气体分子碰撞频率及平均自由程

气体分子在热运动中进行着频繁的碰撞，假如忽略了分子力作用，那么在连续两次碰撞之间分子所通过的自由路程的长短，完全是偶然事件。但对大多数分子而言，在连续两次碰撞之间所通过的自由路程的平均值，即平均自由程却是一定的：是由气体系统自身性质决定的。

不难想象，气体分子的平均自由程与系统中单位体积分子数有关，与分子自身大小有关。事实上，平均自由程的表达式是

为了证明式（8—18），首先应对气体系统和分子作一些简化处理：（1）认为气体分子是刚性球，把两个分子中心间最小距离的平均值认为是刚性球的有效直径，用d表示，并且分子间的碰撞是完全弹性碰撞；（2）系统中气体分子的密度不很大，以致发生三个分子互相碰撞在一起的概率很小，可以忽略，只要考虑两个分子的碰撞过程就足够了；（3）当某个分子与其他分子碰撞时，它们的中心间距为d，可以认为这个分子的直径为2d，而所有与其发生碰撞的分子都视为没有大小的质点。这不改变对碰撞的论证；（4）如果分子热运动的相对速率的平均值为，可以假定这个被跟踪的分子以运动，而所有与其发生碰撞的分子都静止不动。

在上述简化处理下，跟踪分子A，观察它与其他分子碰撞的情形。在分子A的运动过程中，它将扫过一个以πd2为截面积，以其中心的运动轨迹为轴线的圆柱体，凡是处于这个圆柱体内的质点，都将与分子A发生碰撞。因此把截面积πd2称为分子的碰撞截面。这个圆柱体必定是曲折的，如图8—13所示，这是因为在与其他分子发生碰撞的地方，分子A改变了运动方向。在t时间内，分子所扫过的曲折圆柱体的总长度（即其轴线的长度）为2d，相应的圆柱体的体积为。如果系统中单位体积内的分子数为n，那么包含在圆柱体内的分子数为。因为圆柱体内包含的分子都与分子A发生碰撞，所以圆柱体内包含的分子数必定等于在t时间内分子A与其他分子碰撞的次数。若用表示在单位时间内分子A与其他分子的平均碰撞次数，则应有

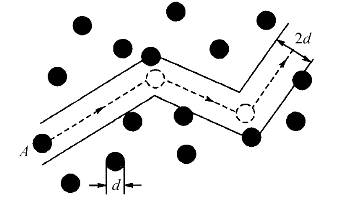
图8—13　分子碰撞次数的计算

式中，为分子的平均碰撞频率。

考虑到分子的实际速率分布后详细计算给出，分子热运动的平均相对速率与平均速率之间存在下面的关系(www.xing528.com)

将式（8—20）代入式（8—21），得

分子A在1s内运动的平均路程为，在这段时间内发生了次碰撞，因而每连续两次碰撞所通过的平均路程，即平均自由程为

上式表示，分子的平均自由程与分子的有效直径的平方成反比，与单位体积内分子数成反比，而与分子的平均速率无关。

由于温度恒定时气体的压强与单位体积内分子数成正比，即p=nkT，所以可以得到分子平均自由程与压强的关系

这表示：在温度恒定时，分子的平均自由程与气体压强成反比。