玻尔兹曼分布律在《大学物理》中的应用

上面讨论了一定量的理想气体在平衡态下分子按速率的分布规律。麦克斯韦速率分布定律没有考虑分子速度的方向，更仔细的讨论应该指出分子按速度是如何分布的，即指出速度分量分别在υx～υx+dυx，υy～υy+dυy和υz～υz+dυz区间的分子数或百分比。这里dυxdυydυz叫速度区间。除了分子按速度分布外，更一般的讨论还需要指出分子按空间位置的分布，即要指出位置坐标分别在x～x+dx，y～y+dy和z～z+dz区间的分子数或百分比。这里dxdydz叫位置区间。因此，从微观上统计地说明理想气体的状态时，以速度和位置表示一个分子的状态就需要指出其分子在dυxdυydυzdxdydz所限定的各个状态区间的分子数或百分比。

在麦克斯韦速率分布函数中，大家可能已经注意到指数因子e-mυ2/（2kT）。由于mυ2/2是分子的平动动能，所以这个因子说明速率分布与分子的平动动能有关。一般情况下，气体分子除具有平动动能，还有势能，势能也会影响气体分子分布。玻尔兹曼（Ludwig Edwgrd Boltzmann，1844—1906）将麦克斯韦速率分布律推广为：在温度为T的平衡态下，任何系统的微观粒子按状态的分布与该状态区间的每个粒子的能量E有关，而且与e-E/kT成正比。这个结论叫玻尔兹曼分布律（Boltznlann Distribution Law），它是统计物理中适用于任何系统的一个基本定律，e-E/（kT）称作玻尔兹曼因子。这个定律说明：在能量越大的区间内的粒子数越小，而且随着能量的增大，区间内的粒子数按指数规律急剧地减少。玻尔兹曼分布律可以写为

式中，分子的总能量等于其动能与势能的和

势能与空间位置有关；n0表示势能为零处单位体积内的分子数。

若对速度不加限制，只考虑分子按空间位置的分布情况，可以把式（8—11）对所有可能的速度积分。

积分式中的被积函数是麦克斯韦速度分布函数，满足归一化条件。定义粒子数密度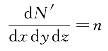，有

作为应用例子，下面计算分子在重力场中按高度的分布。将重力势能Ep=mgh代入上式(www.xing528.com)

式中，m是一个分子的质量，h表示竖直高度，n0就是h=0处的分子数密度。

这个式子说明粒子数密度随高度按指数减少，分子质量越大减少得越快。1909年，法国物理学家佩兰（Jean Baptiste Perrin，1870—1942，曾获1926年诺贝尔物理学奖）用显微镜观测悬浮在不同高度的悬浮微粒数，证实了这个关系式，并且计算出了阿伏伽德罗常数NA。在物理学发展史上，这个实验是证明分子真实存在的最有力的证据。

利用式（8—12）可以解释，在重力场的作用下地球表面附近的大气随高度增加而变得稀薄，以及氢气在高空的相对含量比地面大等现象。将式（8—12）代入理想气体方程p=nkT，即可得在h高度处的大气压强

式中，p0=n0kT是高度为零处的压强。由该式可估算出，每升高10 m，大气压强约降低133 Pa。这就是一种高度计的原理。

由于大气的温度和重力加速度都随高度增加而降低，上面关于地球大气的讨论只在地球表面附近近似成立，实际应用中要加以修正。