统计规律：大学物理概念简介

大量的偶然事件所遵循的规律称为统计规律。例如，色子是密度均匀的正六面体，每个面分别标有1至6点。投掷时，我们不能预先知道色子一定出现哪一点，从1到6都有可能，色子出现哪一点纯属偶然。但是，如果我们投掷的次数很多，出现任意一点的次数几乎相等，约为总次数的1/6。显然，投掷一次，色子出现的点数是偶然的，但是连续大量的投掷，色子点数的出现就显示出一定的规律性。

再看一个演示实验，见图8—6。在一块竖板上部有规律地装上许多小铁钉，竖板下部用小木条隔成等宽等高的狭槽，从板顶中央漏斗处可以投放小球，板前用玻璃块覆盖，使小球留在狭槽内：这种装置叫做道尔顿板（John Dalton，1766—1844）。如果从漏斗入口处投放一粒小球，小球下落时先后与许多铁钉相碰，最后落入某一槽中。重复多次可以发现每一次小球落入哪一个槽中是不能预测的，是完全偶然的，如图8—6（a）所示。如果同时投进大量的小球，就会发现落入各槽的小球的数目是不相等的，且不能预测，但在中央的槽内小球落进最多，两边的槽内落进的小球数目依次减少。如图8—6（b）所示阶梯式图形就是小球按狭槽分布的曲线。重复实验可看出，当小球数量很大时，每次所得的分布曲线都近似一致。也就是说，尽管个别小球落入哪个槽是偶然的，但是大量数目的小球却按槽分布服从一定的统计规律。

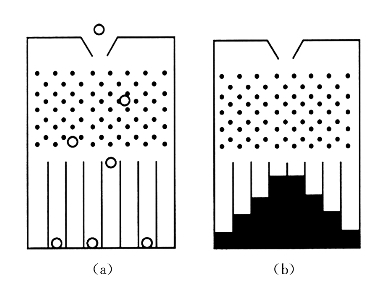
图8—6　道尔顿板实验演示

某个小槽中小球的数目ΔNi占投入小球总数N的比例反映了小球落入该小槽的可能性，因此小球落入第i个狭槽的概率为

小球经多次碰撞后落下来的最后位置x实际是连续向取值的，只不过是狭缝有一定的宽度，使得位置的分类太粗。设想将狭缝宽度减小，数目加多，则小球分布曲线如图8—7（a）所示。在△xi→0的极限情况下，小球分布曲线变得连续光滑，如图8—7（b）所示，则上式中求和变为积分

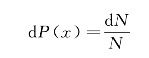
小球落入某一个小槽的概率与小槽的位置和小槽的宽度有关，为此定义一个函数(www.xing528.com)

dP（x）=f（x）dx

f（x）称为小球沿x的概率分布函数（Probability Distribution Function），它表示小球落入x附近单位宽度上的概率，因此也称为概率密度。

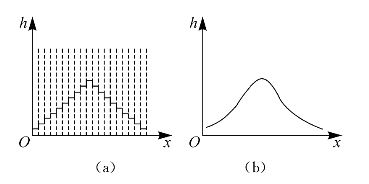
图8—7　小球在槽中的分布曲线

从漏斗入口处投入的小球肯定要落入某个小槽中，即

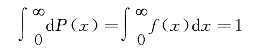
这个式子称为归一化条件，它说明随机事件所有可能取值的概率之和为1。

在上述实验中，只有投入大量小球才能显示出一定的统计规律。因此，统计规律是对大量偶然事件整体起作用的规律，它表现了这些偶然事件整体的本质和必然性，大量偶然构成必然的规律。顺便指出，类似于图8—7（b）的分布，即中间多两边少，是自然界的一种普遍现象，在统计学上称为正态分布（Normal Distribution）。例如人体的身高，大多数人的身高在平均数附近，身材很矮和很高的人都不多。再例如一个班级的考试成绩，特别低分和特别高分的都较少，大多数同学的成绩在平均分数附近。下面将要讨论的气体分子的速率分布也具有这样的特征。