磁场对载流线圈的作用-《大学物理》中的发现

利用安培定律可以分析载流线圈在匀强磁场中所受的力矩作用。图7—18（a）表示一个矩形平面线圈ABCD，其中边长AB=CD=l1，BC=DA=l2，线圈内通有电流I。规定线圈平面法线en的正方向与线圈中的电流方向满足右手螺旋关系。将这个线圈放置在磁感应强度为B的匀强磁场中，并假设线圈的法线en与磁场方向成α角。根据安培定律，AD边和BC边所受磁场力始终处于线圈平面内，并且大小相等、方向相反，在同一直线上，因而互相抵消。而AB边和CD边，由于电流的方向始终与磁场垂直，它们所受磁场力FAB和FCD的大小表示为

FAB=FCD=BIl1

这两个力大小相等、方向相反，但不在同一直线上，因而构成力偶，为线圈提供了力矩，如图7—18（b）所示。此力矩的大小为

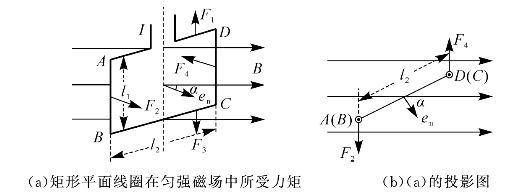
图7—18　矩形平面线圈在匀强磁场中

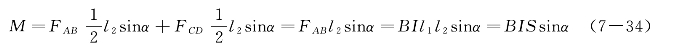
式中，S为线圈的面积，S=l1l2。

将载流线圈的磁矩m=ISen代入式（7—34），得(www.xing528.com)

写成矢量形式为

上式表明：载流平面线圈在匀强磁场中所受力矩的大小正比于线圈的磁矩和磁场的磁感应强度，而力矩的方向可根据右手螺旋关系确定。式（7—36）虽然是从矩形平面线圈推得的，可以证明对于任意形状的平面线圈都适用，也适用于粒子的磁矩。

由式（7—35）可以看到：当α=π/2，即线圈平面与磁场方向平行时，线圈所受力矩最大，在此力矩作用下，线圈将绕通过其中心并平行于AD边的轴转动；当α=0，即线圈平面与磁场垂直时，力矩等于零，线圈达到稳定平衡位置；当α=π时，力矩也等于零，也是线圈的一个平衡位置，但这个位置并不是稳定的平衡位置，稍有扰动就会立即转到α=0的位置去上。

如果载流线圈处于非匀强磁场中，线圈除受力矩的作用外，还要受合力的作用，线圈作为一个整体将向磁场较强的地方运动。