两平行长直电流的相互作用-大学物理

毕奥—萨伐尔定律描述了电流所产生的磁场，安培定律反映了处于磁场中的电流所受力的作用。因此，根据这两个定律，原则上可以处理任意形状载流导线之间的相互作用。但是，无论磁感应强度的计算，还是磁场力的计算，都是矢量的运算，并且需要积分，一般情况下计算比较困难。

下面讨论一种最简单的情形，即两平行长直载流导线之间的相互作用。

设有两根相距为a的平行直导线，分别通以同方向的电流I1和I2，如图7—16所示。如果两导线的间距a与它们的长度相比很小，则可认为它们是无限长的。在电流为I2的导线上取电流元I2dl2，电流I1在电流元I2dl2处产生的磁感应强度为B12的磁场，对I2dl2的作用力为dF12。

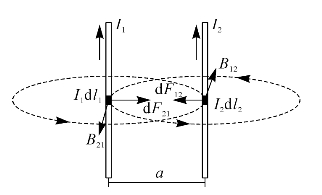
图7—16　同向电流的相互作用

根据安培定律可得

dF12=I2dl2×B12

显然，在假设的情况下，dF12处于两直导线决定的平面内，垂直于导线并指向I1。dF12的大小为

dF12=I2dl2B12

因为导线是平行的，电流I1在电流为I2的导线上各处产生的磁感应强度大小相等、方向相同。所以，无论电流元I2dl2取在导线的什么位置，所受磁场力都是相同的。单位长度所受的力为

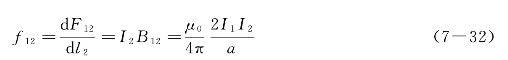(www.xing528.com)

用同样的方法可以求得电流为I1的导线单位长度所受由电流I2给予的作用力f21的大小也为

则f21与f12大小相等、方向相反。

由以上分析可以看到：方向相同的两平行长直电流是相互吸引的。可以证明：方向相反的两平行长直电流必定是相互排斥的（见图7—17）。

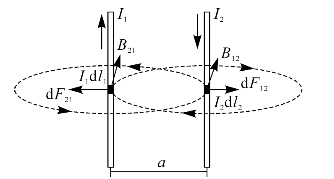
图7—17　反向电流的相互作用

在国际单位制中，电流强度被作为基本物理量，其单位A（安培）为基本单位。

将真空磁导率μ0=4π×10-7N·A-2代入式（7—32），得

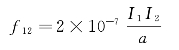
上式中，令a=1m，I1=I2，并调节电流的大小，当f12=2×10-7N·m-1时，导线上的电流就是1A。