大学物理：安培环路定理

在静电场中，电场强度E沿任意闭合环路的线积分为零，说明静电场是保守场。在恒定磁场中，磁感应线是一系列绕电流的闭合曲线，所以磁感应强度B沿任意闭合环路的线积分不恒为零。由毕奥—萨伐尔定律可以导出

这是恒定磁场的基本规律之一，称为安培环路定理（Ampere circuital theorem）。它可表述为：在恒定电流的磁场中，磁感应强度B沿任意闭合环路l的线积分等于环路l所包围的电流强度的代数和的μ0倍。

安培环路定理表明磁场是有旋场。在磁场中不存在像静电场中电势一样的磁势。

为了说明安培环路定理的正确性，我们以载流长直导线的磁场为例，分析磁感应强度B沿任意闭合环路l的线积分。

由式（7—28）知，在无限长载流直导线周围，磁感应强度的大小为

其磁感应线为在垂直于直导线的平面内的同心圆。首先以闭合的磁感应线作为计算B的线积分的闭合环路l，设环路的正向与电流成右手螺旋关系如图7—15（a）所示，则在线积分中，B与df的方向处处一致，且B的大小处处相等，则

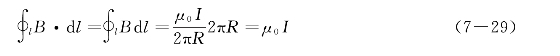
上式说明安培环路定理对此环路是成立的。

图7—15　验证安培环路定理示意图(www.xing528.com)

再选取绕电流I并与其垂直的任意平面闭合环路l来计算B的线积分，如图7—15（b）所示。此时有

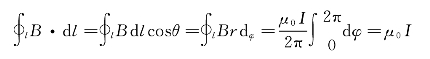
此式表明，当闭合环路l包围电流I时，此电流对该环路上的B的线积分的贡献为dl，即安培环路定理成立。

如果电流的流向相反，则B的方向也与原来相反，上述B的线积分结果等于-μ0I，所以可以对电流的正负做以规定：若电流方向与l的绕向成右手螺旋关系时，电流为正，否则为负。因此，B的线积分的值可以统一用式（7—29）表示。

如果选取的环路l是与电流垂直的任意平面闭合环路，但不包围电流，B的线积分结果又如何呢？此时可以从导线与上述平面的交点作环路l的切线，将l分成l1和l2两部分，取l的绕向如图7—15（c）所示，则沿该环路B的线积分为

此式表明当电流不在闭合环路包围的范围内时，该电流对这一闭合环路B的线积分无贡献。

这里虽只讨论了载流长直导线的情况，并且只讨论了与电流垂直的任意平面闭合环路，可以证明，对非平面的任意闭合环路及任意的恒定电流，安培环路定理均成立。

需要注意的是：安培环路定理中，闭合环路l“包围”的电流是指穿过以闭合环路l为边界的任意曲面的电流，电流的正负依前述规定。而磁感应强度B却是空间所有电流在闭合环路l上产生的磁场的磁感应强度的矢量和。没有被l包围的电流，它们对沿l的B的环路积分没有贡献，可是却对环路l上的磁感应强度B是有贡献的。

在静电场中，利用高斯定理可以方便地计算一些有对称性的带电体的电场分布。这里也同样可以用安培环路定理，计算出某些具有对称性的载流导线周围的磁场分布。

用安培环路定理计算载流导线的磁场分布时，首先要根据电流的对称性分析磁场分布的对称性，然后再由安培环路定理计算磁感应强度B的大小和方向。其中重要的是如何选取合适的闭合环路作为B的积分路径，以使积分中的B能以标量的形式从积分号里提出来。