电容器电容的计算大致可按如下步骤进行:先假设两个极板分别带有+Q和-Q的电量,计算极板间的电场强度;再根据电场强度求出两极板的电势差;最后由极板电量和两极板电势差计算电容。
1.平行板电容器的电容
平行板电容器是由两块彼此靠得很近的平行金属板构成,如图6—19所示。设金属板的面积为S,内侧表面间的距离为d,两极板所带电量分别为+Q和-Q。在极板间距d远小于板面线度的情况下,可以忽略边缘效应,即把平板看为无限大平面,两极板之间的电场可看为匀强电场。若电荷面密度为σ,则两极板间的电场强度大小为
![]()
两极板的电势差为
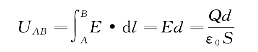
根据式(6—36),平行板电容器的电容为

可见,平行板电容器的电容与极板的正对面积S成正比,与两极板之间的距离d成反比。
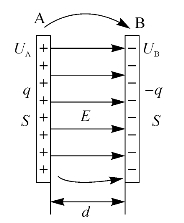
图6—19 平行板电容器
2.同心球形电容器的电容
同心球形电容器是由两个同心放置的导体球壳构成(见图6—20)。设内、外球壳的半径分别为RA和RB,内球壳上带电量为+Q,外球壳上带电量为-Q。根据高斯定理可以求得两球壳之间的电场强度的大小为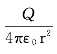 ,其方向沿半径向外。
,其方向沿半径向外。
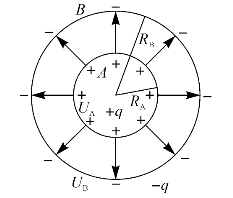
图6—20 同心球形电容器(https://www.xing528.com)
而两球壳间的电势差为
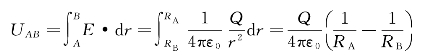
根据式(6—36),同心球形电容器的电容为

3.同轴柱形电容器的电容
同轴柱形电容器是由两个彼此靠得很近的同轴导体圆柱面构成(见图6—21)。设内、外柱面的半径分别为RA和RB,圆柱的长度为l,且内柱面上带正电,外柱面上带负电,内柱面单位长度所带电量为![]() 。当l≫(RA-RB)时,可忽略柱面两端的边缘效应,认为圆柱是无限长的。利用高斯定理可以求得两柱面间的电场强度的大小为
。当l≫(RA-RB)时,可忽略柱面两端的边缘效应,认为圆柱是无限长的。利用高斯定理可以求得两柱面间的电场强度的大小为
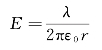
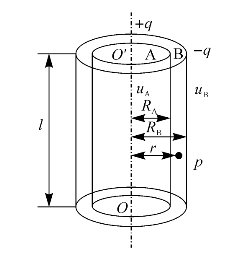
图6—21 同轴柱形电容器
式中,λ是内柱面单位长度所带的电量。
两柱面间的电势差为
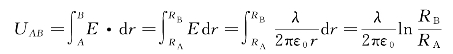
因为内柱面上的总电量为Q=λl,所以同轴柱形电容器的电容为
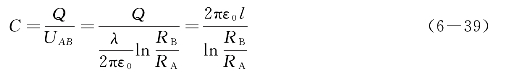
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




