电势与电场强度的关系

电场强度和电势都是描述电场的物理量，它们是同一事物的两个不同的方面，它们之间存在一定关系。实际上，式（6—17）已经反映了这种关系，通过这种关系可以根据电场强度的分布求得电势的分布。可是，在实际问题中往往需要由测得的电势（或等势面）分布情况来估计电场强度的分布情况。因此，在理论上建立一个由电势分布求电场强度的关系式，就变得十分重要。

一个在电场中缓慢移动的电荷，电场力若做正功，该电荷的电势能必定降低；电场力若做负功，该电荷的电势能必定升高。试探电荷q0在电场强度为E的电场中运动位移dl，由于dl很小，在dl的范围内可以认为电场是均匀的。若q0完成了位移dl后，电势增高了dU，则其电势能的增量为q0dU，这时电场力必定做负功，因而有

q0dU=-q0E·dl

即

dU=-Edlcosθ

式中，θ是电场强度E与位移dl之间的夹角。

由此，可以得到

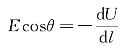
上式等号左边Ecosθ就是电场强度E在位移dl方向的分量，用El表示；而等号右边是电势沿位移方向的变化率，是U沿dl方向的微商，负号表示E指向电势降低的方向。

于是，上面的关系式可以写为

(www.xing528.com)

式（6—25）表示：电场强度在任意方向的分量，等于电势沿该方向的变化率的负值。

为了弄清电势梯度的物理意义，查看如图6—14所示的等势面，其法线方向单位矢量用en表示，指向电势增大的方向。

图6—14　电场和电势的关系

电场强度E的方向沿着en的反方向。电场强度的大小可以表示为

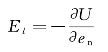
电场强度矢量可以表示为

由此可见：电势梯度是一个矢量，它的大小等于电势沿等势面法线方向的变化率，它的方向沿着电势增大的方向。

由式（6—25）可以得到电场强度的另一个单位，即V·m-1（伏特/米）。