大学物理:真空中的高斯定理应用

高斯定理是反映静电场性质的两条基本定理之一。它给出了通过任意闭合曲面的电场强度通量Φe与闭合曲面内部所包围的电荷量q之间的关系。下面先以点电荷为例来讨论。

设真空中有一个正的点电荷q，置于半径为r的球面中心，如图6—8所示。则由点电荷的电场强度公式可知，球面上各点处的电场强度的大小相等，均为

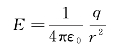
方向沿径矢方向向外。根据电场强度通量的定义式，通过球面S的电场强度通量为

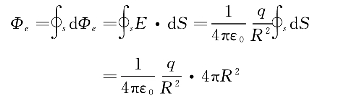
所以

由此可知，通过此球面的电场强度通量等于球面内的电荷量q除以真空电容率ε0，与球面半径无关。

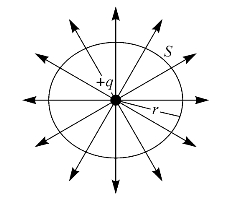
图6—8　点电荷的电场

上面讨论的是点电荷的特殊情况，即包围点电荷的曲面是以点电荷为中心的球面，下面我们来讨论包围点电荷的曲面是任意形状的一般情况。

（1）如图6—9（a）所示，S'是任意闭合曲面，S为球面，S'和S包围同一个点电荷q，两球面之间无其他电荷。根据电场线的连续性可知，凡是通过球面S'的电场线都通过曲面S，所以通过闭合曲面S'的电场强度通量等于通过球面S的电场强度通量，均为。

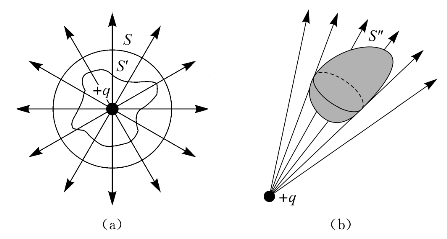
图6—9　高斯定理的证明

由此可知在点电荷的电场中，通过包围q的闭合曲面的电场强度通量与闭合曲面的大小和形状无关，仅与其内所包围电荷的电荷量有关。当q＞0，为正电荷时，Φe＞0，这表示电场线从闭合曲面内穿出；当q＜0，为负电荷时，Φe＜0，这表示电场线从外部穿入闭合曲面内。

（2）若点电荷在闭合曲面外，如图6—9（b）所示，电荷在闭合曲面S"外时，S"曲面可分为两部分看，在下半部S"1上有电场线进入，在上半部S"2上则有电场线穿出。由于从S"2穿出的电场线数目，与从S"1进入的电场线数目相等，所以通过闭合曲面S"的总电场强度通量为零。即

（3）若闭合曲面内存在多个点电荷，则由电场强度叠加原理有

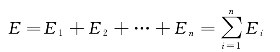
通过闭合曲面的电场强度通量为

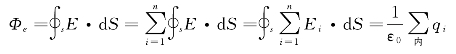
综上所述，真空中高斯定理的内容表述如下。

在真空中，通过任一闭合曲面的电场强度通量，等于该曲面内所包围的所有电荷量的代数和除以ε0。其数学表达式为

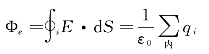(www.xing528.com)

高斯定理中的闭合曲面通常称为高斯面，在理解高斯定理时应注意以下两点。

（1）高斯定理表达式中的电场强度E为闭合曲面上的电场强度，它是由闭合曲面内、外的一切电荷共同产生的合场强。

（2）通过闭合曲面的电场强度通量只由闭合曲面内所包围的电荷决定，与闭合曲面外的电荷无关。

例如，当闭合曲面内无电荷时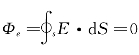，。也就是说，闭合曲面外的电荷对电场强度通量无贡献，但对场强有贡献。

高斯定理反映了静电场的一个基本性质，即静电场是有源场，反映了静电场状态的电场线既有源头，始于正电荷，又有尾闾，止于负电荷。

利用高斯定理，可以计算一些电荷分布具有某种对称性的带电体的场强分布。

例2　求无限长均匀带电直线的电场强度分布。

已知：λ

求：E（r）

解：由于带电直线无限长，且其上电荷分布均匀，所以其产生的电场强度E沿垂直于该直线的径矢方向，而且在距直线等距离各点处的电场强度大小相等，即无限长均匀带电直线的电场分布具有轴对称性。

如图6—10所示，以带电直线为轴线，r为半径，作一高为h的圆柱体，其表面即为高斯面。

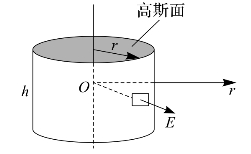
图6—10　无限长均匀带电直线的电场强度

由于电场强度E的方向与上、下底面的法线方向垂直，所以通过圆柱两个底面的电场强度通量为零，而通过圆柱侧面的电场强度通量为E·2πrh，所以通过该高斯面的电场强度通量为

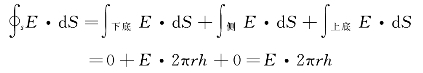
该高斯面所包围的电荷量为

根据高斯定理有

由此可得

即无限长均匀带电直线外某点处的电场强度，与该点距带电直线的垂直距离r成反比，与电荷线密度λ成正比。