电场强度叠加原理及应用

一般来说，空间可能存在由许多个点电荷组成的点电荷系，那么点电荷系的电场强度如何计算呢？下面从力的叠加原理引出电场强度的叠加原理。

如图6—2所示，在点电荷系Q1，Q2，Q3的电场中，在P点放一试验电荷q0，根据库仑力的叠加原理，可知试验电荷受到的作用力为F=ΣFi，因而P点的电场强度为

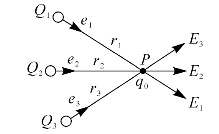
图6—2　电场强度的叠加原理

式中，等式右边的第一项、第二项和第三项分别为Q1，Q2和Q3各自在电场中点P处的电场强度。于是有

E1=E1+E2+E3

因此，可以推广至由点电荷所组成的点电荷系，故可以得出普遍结论如下：点电荷系电场中某点的电场场强等于各个点电荷单独存在时在该点的场强的矢量和。这就是电场强度的叠加原理。其数学表达式为

即

根据电场强度叠加原理，我们可以计算电荷连续分布的电荷系的电场强度。这只是计算电场强度的一种方法，还有其他的方法，以后我们再陆续介绍。(www.xing528.com)

如图6—3所示，有一体积为V，电荷连续分布的带电体，现在来计算点P处的电场强度。首先，将带电区域分成许多电荷元dq，在带电体上取一电荷元dq，其线度相对于带电体V，可视为无限小，从而可将dq看作为一个点电荷。于是dq在P点的电场强度为

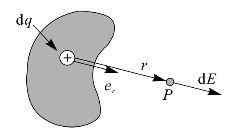
图6—3　点电荷的电场强度

式中，er为由dq指向点P的单位矢量。取电荷元对点P处的电场强度，并求矢量积分。于是可得电荷系在点P处的电场强度

若dV为电荷元dq的体积元，ρ为电荷体密度，则dq=ρdV，式（6-5a）可写成

顺便指出，对于电荷连续分布的线带电体和面带电体来说，电荷元dq分别可表示为dq=λdl和dq=σdS，其中λ为电荷线密度，σ为电荷面密度，则由式（6—5b）可得它们的电场强度为