大学物理：薄膜干涉及劈形薄膜等厚干涉的分析

当一束光射到各向同性的电介质薄膜上，一部分光波会透射，另一部分光波会反射，透射波和反射波的振幅都比原来的要小，于是形象地说成是振幅被“分割”了，所以把薄膜说成是一种分割振幅的干涉装置。普遍地讨论薄膜干涉装置整个交叠区内任意平面上的干涉条纹是一个极为复杂的问题。实际中意义最大的是厚度不均匀薄膜表面的等厚干涉条纹和厚度均匀薄膜在无穷远产生的等倾干涉条纹。这两类干涉条纹的理论比较简单，应用比较广泛，它们是本节讨论的重点。

1.薄膜反射光程差的计算

要研究一束光经薄膜反射和折射后两反射光产生的干涉条纹，首先要计算它们的光程差。

有一束单色光斜射入两个表面相互平行的、厚度为h、折射率为n的薄膜，薄膜两侧的介质折射率分别为n1和n2，如图5—6所示。图中光线1是入射光经薄膜第一个表面反射后，返回至原介质中，光线2是经薄膜第二个表面反射后返回至原介质中。我们来计算光线2和光线1的光程差。由图5—6可知，光程差为

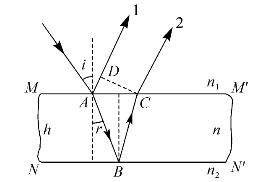
图5—6　平行薄膜光程差的计算

图中的角i为入射光线的入射角，r为折射光线的折射角。由图中的几何关系和光的反射、折射两定律可得

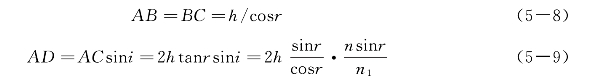
将上两式代入式（5—7）得

或

上述计算还不完全，还要计算所谓的半波损失。为了讨论方便起见，假定n1＜n，n2＜n（或n1＞n，n2＞n）。半波损失是由于两相干光在性质不同的电介质界面MM'和NN'上反射而引起的附加光程差。若把折射率较小的介质称为光疏介质，折射率大的介质称为光密介质，则顺入射光方向看，MM'界面是从光疏介质到光密介质的界面，而NN'界面是从光密介质到光疏介质的界面，两者具有相反的性质。实验和理论证明，光在性质相反的两界面上反射时，两反射光之间产生大小为π的附加相位差，相当于±λ/2的附加光程差。附加光程差的正负号可随意选取，因为两种取法都对应同一相位差π。严格来说，上述附加光程差只具有相对的意义，只有当两反射光相互比较时才谈得上有λ/2的附加光程差。但为简便起见，我们约定：在上、下表面的反射中，若仅有一处有半波损，则在光程差中加上λ/2；若两处都有半波损，则光程差和都没有半波损时的情况一样。

考虑到半波损失，式（5—10）应改成为

上述讨论的入射光斜射入薄膜，经反射和折射后产生的光线2和光线1是相互平行的，它们在无穷远点相干涉。现在我们来讨论薄膜表面上相干涉的两光线的光程差，如图5—7所示。在图中作一根垂直于SA的辅助线AD。在实际的问题中，由于薄膜很薄，点光源S至薄膜的距离较大，A、C两点非常接近，所以可以认为SA≈SD，即SA-SD≪λ。于是光线2和光线1之间的光程差为

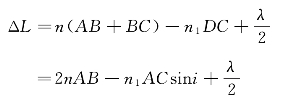
将式（5—8）和式（5—9）代入上式，得

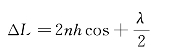
可见，上式和（5—11）式完全相同。

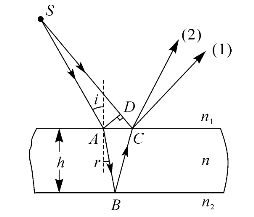
图5—7　平行薄膜表面上

现在我们来计算两表面有一很小夹角α的薄膜表面上光线（2）与光线（1）之间的光程差，如图5—8所示。由于薄膜的夹角α很小，h很薄，A、C两点很接近，可以认为AB≈BC。于是同理可得两光线之间的光程差为

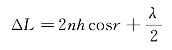
由以上反射的两光线之间光程差的讨论可知，若我们感兴趣的仅是无穷远点和薄膜表面上点的干涉，那么无论是平行薄膜还是劈形薄膜，两光线间的光程差可以统一写成式（5—11）的形式，即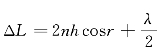。这个公式很重要，在讨论薄膜干涉时要反复使用它，它常常是我们讨论问题的出发点。

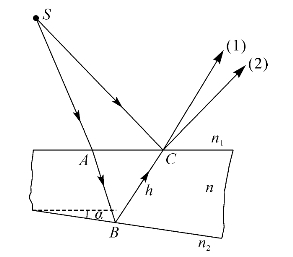
图5—8　劈形薄膜表面上光程差的计算

2.薄膜等厚干涉

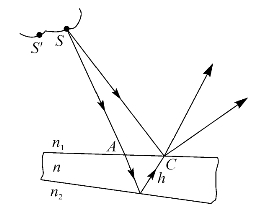
现假定有一劈形状薄膜，如图5—9所示，并假定n2＜n＜n1。若点光源S发出的两条特定光线交于C点，此两反射光在C点的光程差为

ΔL=2nh cosr

若ΔL=kλ或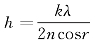，则干涉强度为极大，C点为亮点；若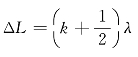或h=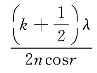则干涉强度为极小，C点为暗点。由以上计算可知，对于点光源S在薄膜表面上不同点，两特定光线间的光程差随薄膜厚度h和折射角r的不同而不同，于是各点的干涉强度各不相同，在表面上形成一套干涉条纹。以上我们假设n2＜n＜n1，说明了在此条件下，不存在半波损失，这并不失去我们讨论问题的普遍性，因为有无半波损失的差别仅仅在于干涉条纹的级数相差半级，即亮、暗条纹位置对调，并不影响条纹的其他特征，如形状、间距、反衬度等。在实际中经常关心的只是条纹的相对变动，只有少数场合需要确定条纹的绝对级数。为了公式和叙述的简捷，今后我们一般不会处理半波损失，只在必要时才予以讨论。

现在再来讨论点光源S邻近的点光源S'（见图5—9）发出的特定光线在薄膜上C点的光程差ΔL'与点光源S发出的两特定光线在C点光程差ΔL之差，即

d（ΔL）=ΔL'-ΔL=d（2nh cosr）=-2nh sinr dr

若|2nhsinrdr|≪λ，则S和S'两点光源在C点产生的干涉强度是相同的，这种非相干的叠加使得薄膜上干涉条纹的反衬度得到提高，干涉条纹更为清晰。

(www.xing528.com)

图5—9　等厚干涉

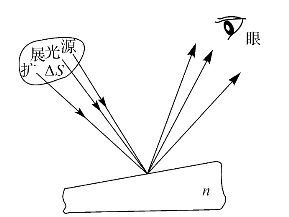
图5—10　扩展光源对等厚条纹的影响

一般在薄膜干涉中使用的是扩展光源（即面光源），面光源上每一点光源在劈形状薄膜上产生一组干涉条纹。于是，薄膜表面总的干涉强度就取决于许许多多组干涉条纹的非相干叠加的结果。在一般情况下，结果是比较复杂的，也难以讨论。但是，如果我们用眼睛垂直注视薄膜表面（通常正是这样观察薄膜的），则观察到的干涉条纹的形状、宽度就容易讨论。由于是接近垂直观察，人眼至薄膜表面的距离远远大于人眼的瞳孔直径，所以面光源发出的光线经薄膜表面反射后不能全部进入眼睛，仅仅是那些满足r≈0的光线可进入眼睛（见图5—10），这部分光线（由面光源上某面元ΔS发出的）在薄膜表面的点的光程差为

|2nh sinrdr|≪λ

所以它们的光程差可写为

由上式可知，如果薄膜内的折射率n是均匀的，凡薄膜厚度h相同的地方，光程差相等，有相同的干涉强度。换言之，同一条干涉亮条纹（或暗条纹）上各点的h相同，这就是等厚干涉条纹名称的由来。所以我们可在劈形状薄膜表面上观察到一组等间距直线条纹，如图5—11所示。

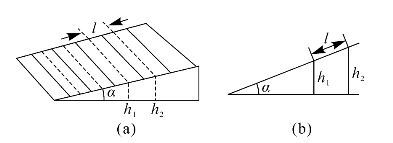
图5—11　等厚干涉条纹宽度计算

若ΔL=2nh=kλ或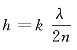，对应亮条纹的位置；若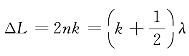或h=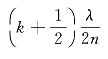，对应暗条纹的位置，其中，k=0，1，2，…

由以上可知，干涉条纹的宽度l为

由图5—11（b）得，

由式（5—13）和式（5—14）得

由于等厚干涉条纹可以将薄膜厚度的分布情况直观地表现出来，它是研究薄膜性质的一种重要手段。科学技术的发展对度量的精确性提出了越来越高的要求，精密机械零件的尺寸必须精确到10-4～10-5cm的数量级，对精密光学仪器零件精确度的要求更高，达10-6 cm的数量级。用机械的检验方法达到这样高的精密度是十分困难的，但光的干涉条纹可将在波长λ的数量级以下的微小长度差别和变化反映出来，这就提供了检验精密机械或光学零件的重要方法，这类方法在现代科学技术中的应用是非常广泛的。

以上讲的光源都是单色的。如果光源是非单色的，则其中不同波长的成分各在薄膜表面上形成一组干涉条纹。由于干涉条纹的宽度与波长有差，因而各色的条纹彼此错开，在薄膜表面上形成色彩绚丽的干涉条纹，这是日常生活中最容易看到的一种光的干涉现象。在水面铺展的油膜，肥皂水泡上以及许多昆虫的翅膀上，都可以看到这种彩色的干涉条纹，在高温下金属表面被氧化而形成的氧化层上，也能看到因干涉现象而出现的色彩，例如从车床切削下来的钢铁碎屑往往呈现美丽的颜色。

3.薄膜等倾干涉

现在讨论平行薄膜上彼此平行的两反射光线在无穷远处产生的干涉条纹。如果用凸透镜观察，干涉条纹将形成在它的后焦面上，如图5—12所示。根据透镜的物、像间等光程性和式（5—13），图5—12中的两反射光线2和1在幕上P点的光程差为

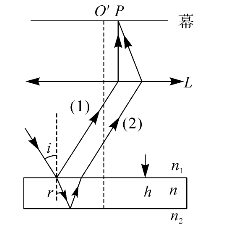
图5—12　等倾干涉光程差

由上式可知，如果薄膜内部的折射率是均匀的，再加上讨论的薄膜厚度h也是均匀的，所以引起ΔL变化的唯一因素是折射角r（也即入射角i），说明i是入射角相同的光线对应同一干涉条纹，等倾干涉条纹的名称即由此而来。观察等倾干涉条纹的实验装置如图5—13所示。由于幕上一点P到幕中心O点的距离只决定于倾角，所以具有相同倾角的反射线（如图5—13所示，它们排列在一圆锥面上），在幕上交点的轨迹将是以O为中心的圆周。于是我们在幕上可观察到一组以O为中心的明暗相间的圆形条纹。

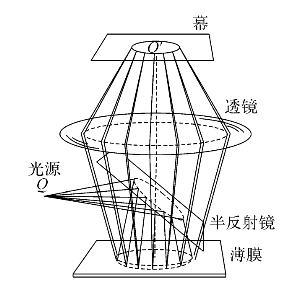
图5—13　等倾干涉条纹观察

现在再来分析等倾干涉条纹的一些特点。由式（5—16）可知，r角越小（也即入射角i越小），光程差ΔL越大，从而对应的条纹级数越高。所以在幕上半径小的圆条纹级数要比半径大的圆形条纹级数高。r=0（即i=0）时，对应图5—13幕上中心点O的光程差最大，它究竟是暗点还是亮点，或既非亮点也非暗点的情况，要由n1，n2，n3和h的情况决定。关于条纹疏密情况也可用式（5—16）进行讨论。对该式进行微分，并使它等于λ，即

由上式可得两相邻亮（或暗）干涉条纹间的角距离为

上式说明了r角越大（也即i角越大），|dr|就越小，即半径越大的那些干涉条纹之间的距离越小，也就是离中心点O远的地方条纹比较密，离中心点O近的地方条纹比较疏。式（5—18）还说明了，若膜的厚度过厚，即h过大，|dr|极小，干涉条纹过密，难于分辨清楚，所以要观察到薄膜的干涉条纹，膜的厚度是有限制的。

最后，来讨论当膜厚度h做连续变化时，干涉条纹的变化情况。出发点还是式（5—16），中心点O的光程差ΔL=2nh，每当改变λ/2时，ΔL改变了一个波长λ，中心点的级数改变1。设原来膜的厚度，中心点的级数为k，从中心算起的第1，2，3，…条纹级数为k-1，k-2，k-3，…。当h增大到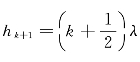时，中心点的级数成为k+1，从中心点算起的第1，2，3，…根条纹的级数顺序为k，k-1，k-2，…。原来的中心斑点变成第一圈，原来的第一圈变成第二圈……。同时在中心生出一个新的斑点。所以当h连续增大时，我们看到的是中心强度周期地变化着，由于这里不断生出新的条纹，犹如泉口的水波似的发散出去。对于h连续减小的情况可做同样的分析，这时看到的景象恰好与上面相反，圆形条纹不断向中心会聚，直到缩成一个斑点后在中心消失掉。由于中心强度每改变一个周期（即吐出或吞进一个条纹）就表明薄膜厚度改变了半个波长，利用这种方法可以精确地测定h的改变量。

如图5—13所示观察等倾于涉条纹的实验装置中的光源是扩展光源。扩展光源上各个点光源在透镜焦面的幕上形成的各套干涉条纹是完全重合的，它们非相干叠加的结果将使亮纹更亮，暗纹依然是暗的，条纹变得更为清晰。所以在观察等倾干涉条纹，扩展光源是有利而无害的。若光源是非单色性的，例如日光，由于不同波长的光，薄膜有不同的折射率，由式（5—16）可知，即使在h和角r相同情况下，不同波长的两反射光线的光程差ΔL也不相同，于是在透镜后焦面上可观察到彩色的圆形条纹。对于半径较大的干涉条纹或膜的厚度h稍厚而使各种波长的干涉条纹重叠在一起，致使干涉条纹无法辨认。