杨氏实验的重要地位与作用：简化装置，产生明暗相间的干涉条纹

两个普通的独立光源照射在同一空间区域（如屏幕）时，强度将是简单的相加，这种现象是屡见不鲜的。但在一定条件下，在两束光重叠区域内不是简单的叠加而是有的加强有的削弱，即呈现亮暗相间的条纹，这就是光的干涉现象。光的干涉在牛顿时代已观察到（牛顿环），但首先用实验实现光的干涉是杨氏。杨氏实验在光学发展史上具有极其重要的地位，它是历史上以光的干涉现象揭示光的波动性的第一个实验，它是由英国医生、物理学家托马斯·杨在1801年完成的。杨氏用惠更斯原理和波的叠加原理完美地解释了他的实验结果，第一次测定了光波波长。杨氏实验不仅在历史上有着重要地位，而且至今还起着重大的作用。

1.杨氏实验装置

杨氏当初做的实验装置如图5—2所示。先让日光照射阻挡屏M1上针孔S，阻挡屏M2上也有两个相距很近的针孔S1和S2。M1、M2和屏幕M3是相互平行的，M3和M2的间距以及M2和M1的间距均远远大于S1和S2的间距。在M3上可以观察到一组明暗相间的、几乎是平行的直线彩色条纹。

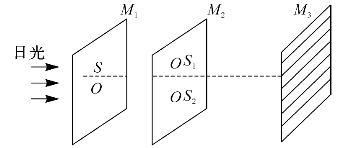
图5—2　原杨氏实验装置

后来发现，以狭缝代替S、S1和S2针孔，并用单色光（例如钠黄光）照射，在屏幕上可得到更为清晰的明暗相间的单色直线条纹，装置如图5—3所示。自20世纪60年代激光源产生后，杨氏实验装置更为简单。若单色光采用激光，则图5—3中的S狭缝可去除，在屏幕M3上同样可观察到清晰的明暗相间的直线条纹。

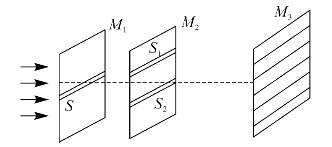
图5—3　杨氏双缝干涉

杨氏实验的结果，即在M3上观察到明暗相间的条纹是无法用几何光学理论来解释的，因为几何光学告诉我们光是沿着直线传播的，那么图5—2或图5—3中的M3上应是一片黑暗，根本不可能有光，但事实上屏幕上有光且光强是周期分布。如何来解释此实验现象呢？这正是我们下面要讨论的内容。

2.光强分布

现在从惠更斯原理和波的叠加原理作为出发点来研究M3上呈现的光强分布。将图重新画在下面。用单色光照射针孔S，将S看作是一个点光源，它向空间发出球面波，这样针孔S1和S2必落在S发出的球面波波面上（若图5—4中的R1=R2，则落在同一波面上）。

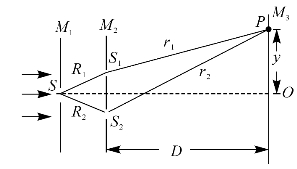
图5—4　杨氏干涉原理图

由惠更斯原理，S1和S2可视为新的次波源，S1和S2各自向空间发出球面波，它们在M3相遇，可根据波的叠加原理进行计算。假定单色光的波长为λ。点光源的振动写为(www.xing528.com)

次波源S1的振动写为

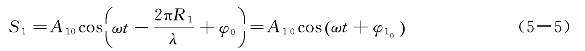
次波源S2的振动写为

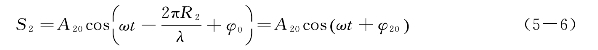
由于在杨氏实验中，有条件d≪D（例如d=0.5 mm，D=100 cm），所以r1和r2几乎是平行的，这样S1和S2发出的球面波在P点相遇时，它们的振动方向可看作是平行的，于是在P点两振动的叠加是属于同频率、同振动方向的两个简谐振动的合成。

3.干涉条纹的形状

前面提到，在图所示的屏幕M3上，在通常的实验观察的线度内，可观察到明暗相间的直线条纹，我们现在要问，为什么干涉条纹是直线条纹？如果屏幕M3放在其他位置。将观察到怎样形状的干涉条纹呢？要回答这些问题，还需从两个相干点光源S1和S2在空间干涉情况谈起，见图5—5。

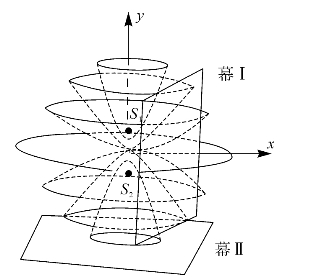
图5—5　两相干点光源的干涉场

我们已证明：当r2-r1=kλ时，干涉强度有极大值，当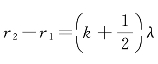时，干涉强度有极小值；当r2—r1=常量时，那些点的干涉强度相等。

根据几何学知道，当r2—r1=常量的轨迹是以S1和S2为焦点，S1和S2的连线为旋转轴的双叶旋转双曲面。图5—5是通过S1和S2的一个垂直剖面图。图5—5的幕Ⅰ与双叶旋转双曲面相截，在幕Ⅰ上的截线为双曲线。所以，一般来说在幕上观察到的干涉条纹应为双曲线，但是如果幕Ⅰ与S1和S2的距离远远大于S1和S2的距离，而同时在幕Ⅰ上的观察范围不是很大的话，在幕Ⅰ上观察到的干涉条纹近乎是直线，我们在前面所说在幕上观察到直线条纹就是这个含义。

如果图5—5的两相干点光源S1和S2向全空间发出光波，则在幕Ⅱ上可观察到一组明暗相间的同心圆形干涉条纹。但是在杨氏实验里的S1和S2不是向全空间发出光波，只向图中的右方发出半个球面波，于是在幕Ⅱ的位置，一般来说，可观察到一组明暗相间的同心圆弧干涉条纹。