光的相干性概述-《大学物理》成果

在讨论机械波时已知两列波相遇发生干涉现象的条件：振动频率相同、振动方向相同和相位差恒定。但实验发现，从两个独立的同频率的单色普通光源发出的光相遇，却不能得到干涉图样，下面对此做一简单的分析。

设两个振动方向相同、频率相同的单色光在空间某一点相遇，它们的光矢量的大小分别为

E1=E10cos（ωt+φ10），E2=E20cos（ωt+φ20）

叠加后合成的光矢量的大小为E=E1+E2。从而合成光矢量的量值为

E=E0cos（ωt+φ0）

式中

在观测时间内，平均光强I正比于E2的时间平均值，即

如果这两束同频率的单色光分别由两个独立的普通光源发出的，由于光源中原子或分子发光的独立性和随机性，两光波间的相位差Δφ也将随机地变化，并等概率地取0～2π的所有值。因此。在所观测的时间内

由此得

即(www.xing528.com)

式（5—1）表明两束光重合后的光强等于两束光分别照射时的光强I1和I2之和，把这种情况称为光的非相干叠加。

如果这两束光来自同一光源而使它们的相位差始终保持恒定，则其合成后的光强为

此时cos（φ20-φ10）将不随时间而变，被称为干涉项，这种情况称为光的相干叠加。

由式（5—2）可知，由于两光束间存在着相位差，合成后的光强不仅取决于两束光的光强E1和E2，还与两束光之间的相位差Δφ有关。当两束光在空间不同位置相遇时，由于在这些位置离光源的距离不同，因此其相位差Δφ也将不同，在空间各个不同点处的光强将发生连续变化，即光强在空间重新分布。

当Δφ=±2kπ（k=0，1，2，…）时，，在这些位置光强最大，称为干涉相长。当Δφ=±（2kπ+1）（k=0，1，2，…）时，，在这些位置光强最小，称为干涉相消。如果I1=I2，那么合成后的光强为

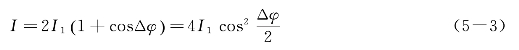
光强I随相位差△φ的变化情况，如图5—1所示，这就是光的干涉现象。

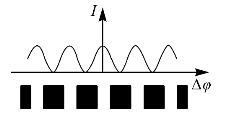
图5—1　光的干涉现象

综上所述，我们把能产生相干叠加的两束光称为相干光，相干叠加必须满足振动频率相同、方向相同、相位差恒定的条件。只有从同一光源的同一部分发出的光，通过某些装置进行分束后，才能获得符合相干条件的相干光。在实验中，为了获得明显清晰的干涉现象，参与叠加的两束光除了要满足上述相干条件外，两束光的强度也不能相差太大。