大学物理-波的强度及能流密度

为了描述介质中的能量分布情况，引入能量密度，定义介质单位体积内的能量称为波的能量密度，用ω表示。

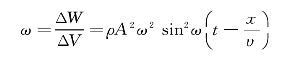
能量密度在一个周期内的平均值叫作平均能量密度，用表示。

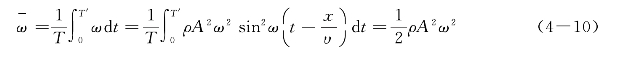
式中，T'为能量密度ω变化的周期，其值为位移x变化周期的，即。式（4—10）中虽然是由平面简谐波推导出来的，但它适用于各种弹性波（依靠介质的弹性作用而传播的波）。这是因为介质中同样的运动状态应该有同样的能量，与波面的形状无关。公式中的振幅A应理解为所在点的振幅。

为了描述波动过程中能量的传播，引入能流密度的概念。能流密度是一个矢量，用P表示。它的大小是单位时间内通过垂直于波的传播方向的单位面积的能量，它的方向是能量传播的方向，即波速的方向。能流密度在一个周期内的平均值叫平均能流密度，也叫波的强度，用I表示。J在光学中叫光强，在声学中叫声强。

如图4—6所示，在介质中取一垂直于波的传播方向的面积S，由于能量的传播速度就是波速，所以单位时间内通过S的能量为ωSυ。

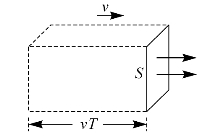
图4—6　能量密度与能流密度的关系

由定义可知，能流密度

上式两边取时间平均值，得波的强度

(https://www.xing528.com)

式（4—11）和（4—10）式一样，也适用于球面简谐波。以下利用式（4—11）来讨论一下球面简谐波的振幅。

设球面简谐波在无吸收的介质中恒定传播，在介质中任取两波面，半径分别为r1和r2，面积分别为S1和S2，两波面上的能流密度分别为I1和I2。

由于介质不吸收振动的能量，所以单位时间内通过两波面的能量相同，则

利用式（4—9），有

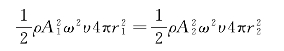
整理得

A1r1=A2r2

改写成

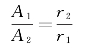
由此可见，球面简谐波的振幅与到波源的距离成反比。