简谐振动的基本特征-《大学物理》

简谐振动是最简单也是最基本的振动形式，任何一个复杂的振动都可以由多个不同频率的简谐振动叠加而成。下面以弹簧振子为例，研究简谐振动的运动规律。

在光滑的水平面上，有一个一端被固定的轻弹簧，弹簧的另一端系一小球，如图3—1（a）所示。当弹簧呈自然伸长状态时，小球在水平方向不受力的作用，小球所在的位置O，称为平衡位置。若将小球向右拉伸x，弹簧被拉长，如图3—1（b）所示。这时小球受到弹簧所产生的方向指向点O的弹性力F的作用。将小球释放后，小球就在弹性力F的作用下左右往返振动，并可以永远振动下去。由轻弹簧和物体构成的这个振动系统，由于弹簧质量可以忽略不计，它只提供物体做周期振动所需要的回复力，而物体质量集中于它的质心，具有一定的惯性，可以等效为一质点，这种系统称为弹簧振子。

图3—1　弹簧振子做简谐振动的示意图

为了描述小球的这种运动，取小球的平衡位置O为坐标原点，通过点O的水平线为x轴，如图3—1所示。如果小球的位移为x，则它所受弹性力F可以表示为

根据牛顿第二定律有

即

加速度a与位移的大小x成正比，而方向相反，人们把具有这种特征的运动称为简谐

振动。

由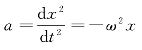积分可得简谐振动的运动方程为(www.xing528.com)

式中，积分常量A和φ分别称为振幅和初相位。

振动的速度和加速度分别为

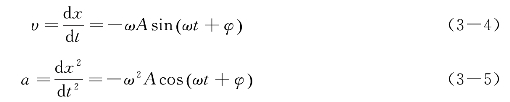
由上式可知：物体做简谐振动时，它的位移、速度和加速度都是在做周期件变化的，变化曲线如图3—2所示，称为简谐振动曲线。

图3—2　简谐振动曲线

上面分析了由轻弹簧和小球所组成的弹簧振子做无摩擦振动的例子。弹簧振子的振动是典型的简谐振动，它表明了简谐振动的基本特征。从分析中可以看出，物体只要在F=-kx的线性回复力的作用下运动，其位移必定满足微分方程式（3—2），而这个方程的解式（3—3）就一定是时间的余弦（或正弦）函数。简谐振动的这些基本特征在机械运动范围内是等价的，其中任何一项都可以作为判断物体是否做简谐振动的依据。但是，由于振动的概念已经扩展到物理学的各个领域，任何一个物理量在某定值附近做往返变化的过程都属于振动，于是可对简谐振动做如下普遍定义。

任何物理量的变化规律若满足方程式

此式决定于系统自身的常量，则该物理量的变化过程就是简谐振动。