大学物理：陀螺仪进动现象及回转效应

现在介绍陀螺仪（回转仪）受外力矩作用时产生的回转效应。在这种情况下，陀螺仪的转动轴并不固定。如图2—13所示为一杠杆陀螺仪，杠AB可绕光滑支点O在水平面内自由转动，也可以偏离水平面而倾斜。同样，陀螺仪G是一个厚重的对称转子，其转动惯量非常大，重物W置于杠的另一端，与陀螺仪G平衡。若向外移动重物W，杠AB当然会偏离水平面而倾斜。如果让陀螺仪G绕自身的转轴高速旋转起来，再向外移动重物W，我们看到，杠AB不会偏离水平面，而是在水平面内绕铅直轴OO'旋转起来。这种高速自旋的物体的轴在空间转动的现象叫进动。这种陀螺仪在外力矩的作用下产生的进动效应，称为回转效应。

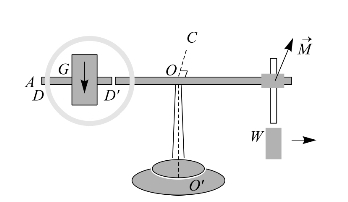
图2—13　进动现象

为什么陀螺仪的轴AB在重力的作用下不向下倾斜而绕铅直轴OO'转动呢？这可以用角动量定理式加以解释。当陀螺仪高速绕自己的轴旋转时，它的角动量为，方向沿杆AB，图中向右（在水平面内）。向外移动重物W，杠AB失去平衡，其重力矩应是沿OC方向的（图中在水平面内与杠AB垂直，也与陀螺仪转子的角动量L垂直），俯视图中，M为逆时针方向。

将式写为矢量式，可得出在dt时间内陀螺仪转子对支点的自旋角动量矢量的增量为

因此，dt的方向与相同，也为逆时针方向，在水平面内。经过时间Δt后，陀螺仪转子的角动量变为，既然这增量在水平面内，所以飞轮的角动量仍然在水平面内，其大小不变，但方向发生了改变，因此，杠AB不会向下倾斜，而是要在水平面内逆时针旋转了。杠AB绕铅直轴OO'（称为自旋轴）继续不断地逆时针旋转就形成了进动。这就是说进动现象正是自旋的物体在外力矩的作用下沿外力矩方向改变其角动量矢量的结果。

在图2—14中，由于陀螺仪转子所受的力矩的大小不变，方向总是水平地垂直于L，所以进动是匀速的。从图2—14可以看出，在dt时间内自旋轴转过的角度为

而相应的角速度叫进动角速度，为(www.xing528.com)

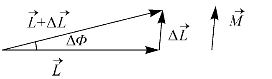
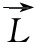图2—14　和Δ方向示意图

小孩玩的陀螺的回转效应是有目共睹的。在不旋转时，陀螺受到重力矩的作用便倾倒下来。当使它绕自己的对称轴高速旋转时，即使轴线已倾斜，它也不会倒下（见图2—15）。这时陀螺除绕它的自转轴转动外，自转轴还将绕竖直轴Oz回转，该竖直轴通过陀螺尖顶与地面O处接触。陀螺的这种进动也是重力矩作用的结果。不难证明，这时陀螺进动的角速度，即它的自转轴绕竖直轴转动的角速度，可按下式求出

其中，θ为陀螺的自转轴与竖直轴之间的夹角。

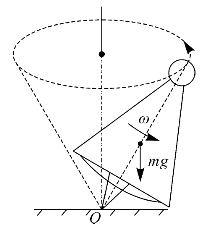
图2—15　陀螺的进动