刚体定轴转动的角动量，大学物理

1.刚体定轴转动的角动量

如图2—11所示，有一刚体以角速度ω绕定轴Oz转动。由于刚体绕定轴转动，刚体上每一个质点都以相同的角速度绕轴Oz做圆周运动。

图2—11　刚体定轴转动的角动量

其中，质点mi对轴Oz的角动量为，于是刚体上所有质点的角动量，即刚体对定轴Oz的角动量为

式中，为刚体绕轴Oz的转动惯量J。于是刚体对定轴Oz的角动量为

2.刚体定轴转动的角动量定理

从式（2—25）可以知道，作用在质点mi上的合力矩Mi应等于质点的角动量随时间的变化率，即

而合力矩Mi中含有外力作用在质点mi的力矩，即外力矩，以及刚体内质点间作用力的力矩，即内力矩。

对绕定轴Oz转动的刚体来说，刚体内各质点的内力矩之和应为零，即，故由上式，可得作用于绕定轴Oz转动刚体的合外力矩M为

亦可写成

上式表明，刚体绕某定轴转动时，作用于刚体的合外力矩等于绕此定轴的角动量随时间的变化率。式（2—27）是转动定律的另一表达方式，但其意义更加普遍。即使在绕定轴转动物体的转动惯量J因内力作用而发生变化时，式（2—27）仍然成立。这与质点动力学中，牛顿第二定律的表达式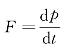较之F=ma更普遍是一样的。

设有一转动惯量为J的刚体绕定轴转动，在合外力矩M的作用下，在时间Δt=t2-t1内，其角速度由ω1变为ω2，由式（2—27）积分得

式中，是外力矩与作用时间的乘积，叫作力矩对给定轴的冲量矩，又叫角冲量。

如果物体在转动过程中，其内部各质点相对于转轴的位置发生了变化，那么物体的转动惯量J也必然随时间变化，若在Δt时间内，转动惯量由J1变为J2，则式（2—28）中的Jω1应改为J1ω1，Jω2应改为J2ω2。于是下面的关系式是成立的，即

式（2—29）表明，当转轴给定时，作用在物体上的冲量矩等于角动量的增量，这一结论叫作角动量定理。它与质点的角动量定理在形式上很相似。

3.刚体定轴转动的角动量守恒定律(www.xing528.com)

当作用在绕定轴转动的刚体上的合外力矩等于零时，由角动量定理也可导出角动量守恒定律。

由式（2—29）可以看出，当合外力矩为零时，可得

这就是说，如果物体所受的合外力矩等于零，或者不受外力矩的作用，物体的角动量保持不变。这个结论叫作角动量守恒定律。

必须指出，上面在得出角动量守恒定律的过程中受到刚体、定轴等条件的限制，但它的适用范围却远超出这些限制。

有许多现象都可以用角动量守恒来说明。

有一人坐在能绕竖直轴转动的凳子上（摩擦忽略不计）。开始时人平举两臂，两手各握一哑铃，并使人与凳一道以一定的角速度旋转。由于在水平面内没有外力矩作用，人与凳的角动量之和应当保持不变，因此，当人放下两臂，使转动惯量变小时，人与凳的转动角速度就要加快。又如花样滑冰运动员表演旋转时，先把两臂张开，并绕通过足尖的垂直转轴以角速度ω0旋转，然后迅速把两臂和腿朝身边靠拢，这时由于转动惯量变小，根据角动量守恒定律，角速度必增大，因而旋转更快。跳水运动员常在空中先把手臂和腿蜷缩起来，以减小转动惯量而增大转动角速度，在快到水面时，则又把手、腿伸直、以增大转动惯量而减小转动角速度，并以一定的方向落入水中。

【例题2】如图2—12所示，一个质量为m的物体与绕在定滑轮上的绳子相连，绳子质量可以忽略，它与定滑轮之间无滑动。假设定滑轮的质量为M、半径为R，滑轮轴光滑。试求该物体由静止开始下落的过程中，下落速度与时间的关系。

解：如图2—12所示，选取向下为坐标轴正向，设物体下落的加速度为a，滑轮转动的角加速度为α，根据牛顿第二定律和刚体定轴转动定律，有

对于m

mg-T=ma

对于M

TR=Jα

又因为

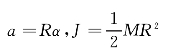
联立以上三式解得

可见物体做匀加速直线运动。

由初始条件υ0=0，得

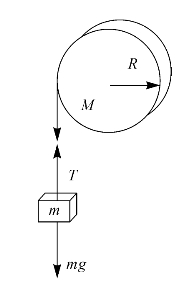
图2—12　例题2示意图