大学物理刚体定轴转动

定轴转动刚体上各点都在绕固定轴做圆周运动，圆周轨道所在平面垂直于转轴，这个平面称为转动平面，圆轨道的中心就是转动平面与转轴的交点O，称为转心。刚体上各点（或质元）的半径（ri）不等、速度υi不同，但是刚体上各点半径在相同的时间间隔内都转过相同的角度。

刚体绕某一固定轴转动时，各质元的线速度、加速度一般是不同的，如图2—6所示。但是，由于各质元的相对位置保持不变，所以描述各质元运动的角量，如角位移、角速度和角加速度都是一样的。描述刚体转动时，采用角量较为方便。从刚体定轴转动的特点可知，在刚体内平行于转轴的直线上各点的运动情况完全相同，因此，该直线上的一点就可以代表该直线的运动。假想用一个与加速度与转轴垂直的平面截取刚体，得到一个截面S，若知道截面S各点的运动，那么整个刚体上各点的运动情况就都可以知道，因此，就可以用截面S代表定轴转动的刚体。

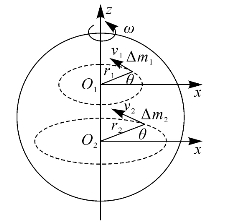
图2—6　刚体转动的线速度与加速度

1.刚体转动的角速度和角加速度

定轴转动刚体在任意时刻的位置可以用角坐标表示

式（2—5）即为刚体绕固定轴转动的运动学方程。

若用dθk表示刚体在dt时间内转过的角位移，其角速度矢量为，大小为|ω|=，而方向则规定为沿转轴的方向，具体指向由右手螺旋法则确定。角位移△θ的正负：面对z轴看，逆时针方向转动，Δθ增大，Δθ取正；顺时针方向转动，θ减小，△θ取负。

刚体定轴转动的角速度沿其转轴方向，所以，可以简化为标量，即

定轴转动中可用Δθ的正负表示转动方向。

角加速度为

(www.xing528.com)

距离转轴为r的质元，其线速度和刚体的角速度的关系为

其线加速度与刚体的角加速度及角速度的关系为

2.匀变速转动

刚体定轴转动的一种简单情况是匀变速转动。在这种转动过程中，刚体转动的角加速度保持不变。以ω0表示刚体在t=0时的角速度，以ω表示刚体在t时刻的角速度，以θ表示刚体在0到t时刻的角位移，类比匀速直线运动，可推导出相应的公式

【例题1】一个刚体以60r/min的转速绕z轴做匀速转动（ω沿z轴正方向）。设某时刻刚体上一点P的位置矢量为r=3i+4j，其单位为cm，若以1.0cm·s-1为单位速度，则该时刻P点的速度为（　）

（A）υ=94.2i+125.6j；　（B）υ=-23.1i+18.8j

（C）υ=-25.1i+18.8j；　（D）υ=31.4k

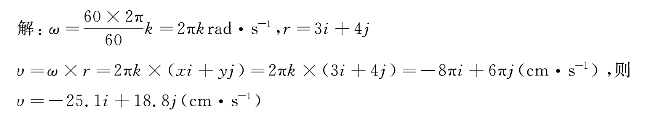
故（C）正确。