中国著名量子物理学家的前沿思维解读，实用趣味引领量子力学

为了把我们介绍的不同观点说得更明白一点，让读者有浅尝辄止的感觉，我们将要重述量子力学的基本假设。这些假设极其的数学化，读者可以赤裸裸地忽略以下内容的存在，而也许只有这样，我才能放开手脚，写给有兴趣继续深入的小众。

所以接下来读这本书的逻辑，我假设读者不是数学和物理专业的，但有基础的理科背景。如果是这两个专业的，在了解这一章所讲述的逻辑结构以后，可以找深度更合适的来读。对于非这两个专业的读者而感兴趣的，我也无法用文字来描述清楚这些数学的概念。所以，既然可以相信假设，比如我们接纳了光速不变和协变性假设，我们就可以开始讨论狭义相对论，如果你相信这两条之上还需要有假设来创造这两条假设，那么可以归于上帝存在，上帝创造了假设。而这里，为了让我们的讨论可以继续下去，读者就要暂时“迷信”我说的结论，而不要在这本书的难度和范畴里讨论深入的细节，姑且把它当作讨论的假设。再深入，过去一百多年里的物理学实验和理论的发展奠定了足够的基础，尽管去相信好了，不必质疑。如果读者真的好奇而质疑的话，不要用这本书的证据和论证作为质疑的根据，它本来就不是一本专业的教材和论文集，向下深究需要足够的数学基础和物理学训练，我们这些讨论的内容作为假设接受即可。

量子系统里任何有物理意义的东西，被认为全都包含在其数学结构的状态矢量之中。但有一点必须强调，量子理论具有概率性质，体现在状态矢量中的许多信息都以概率密度的形式给出，而概率密度由状态矢量的模平方导出。我们用状态矢量的模平方而非平方，是因为状态矢量自身可能是复数，这源于其“波”的一面，而概率密度若要表示系统某种可观察性质，它的值必须是实数。

量子力学的概率解释要求大量同等制备的粒子展现出一种分布概率。这个概率体现了粒子在这里或在那里被发现的概率更高。在多次测量后可得到一张概率随空间坐标分布的地图。如果我们想要知道在空间某特定位置发现一个粒子的概率，在这一位置发现粒子的概率为零，它必须在这周围有个小的空间来容纳这一粒子。当我们讲某一位置的概率密度时，意味着这一位置附近的小体积，我们把它叫体积元，那就须由状态矢量计算得到的概率密度乘以该处的体积元，这类似于通过质量密度乘以体积得到某物体的质量。这些概率是对个别量子粒子而言的，所以整个空间里概率之和应等于1，这个粒子必定会在某处，即归一化条件。由此可以知道，为了让这张概率地图有足够的清晰度，事实上我们需要对同样状态的量子系统重复测量。这也说明，一个量子的概率波方程，需要无穷多次的经典测量的结果才能更清晰知道它的所有可能。

这是一个重要的推论，它告诉我们，除非在一些非常特别的情况下，为了精确描述一个量子的状态，我们需要足够次数的多经典的测量结果来获得足够的近似。但由于可能的非线性效应存在，“小概率”而“大影响”，任何一个“经典信息”都会具有同等可能的重要性，而不可以被统计平均掉。我们还是要强调这不是推论或证明，只是为了让读者有更深的印象。斯大林说死一个人是悲剧，死一百万人是数字。在量子世界里，每次事件都有可能是“伟大”的。与经典统计不一样的是，事件不能因为概率小而被忽略。因此，为了完整地描述一个量子信息态，我们需要无穷多的经典信息。

薛定谔波动方程可在经典波动方程中使用德布罗意关系导出。基于薛定谔方程求解而得到的概率分布，可以将经典的系统总能量（势能与动能之和）、动量用它们在量子力学中的等价算符代替，而得到某一概率分布下的平均能量、动量和其他物理量。这样，量子理论的描述根植于一种数学方法，这种数学方法用适当数学算符来表达为了获取系统某个物理量而采取的测量，而最终获得某一数值的概率。量子理论非常严格地强调了“测量”在理论中的重要性，为了反映这一点，物理量常称为观察量。我们于是有了第二个假设。

量子理论的每一个观察量都有一个与之对应的算符；反之，每一个算符都对应于一个观察量。可是实际上，对于很多算符，很难设想实际进行测量所需的装置。所以人们感兴趣的大多数计算只为获得为经典物理所能理解的“标准”观察量，如位置、动量、角动量以及能量所对应的算符。理论与真实世界里的可观察量相联系的必要性还限制了算符本身的结构。算符必须是线性的，必须符合某种结合规则，算符的本征值是实数，而且只有实数才能够表示观察量的值。比如我们在经典物理里常说的质量，如果我们把量子粒子的质量视为一种观察量，那么应当承认在大学所传授的常规的量子理论里没有质量算符。但是实际上更高深的量子处理中确有质量算符，应用它可以得到基本粒子的质量，这就需要希格斯玻色子了。这把我们引向第三个假设。

假设3强调了量子理论的概率性质。我们常将在一系列同等制备的量子粒子上重复测量的结果解释为获得了集中于观察量均值周围的一个分布。而且，只有进行无穷多次测量时，概率分析中的期望值才能给出真正的均值。如果状态矢量是算符的本征态，期望值正好就是相应的本征值。当然，这些量不能再用普通的数学来表示。它们要么是矩阵力学，要么是算符动力学或基于矢量空间的量子理论。我们从线性代数里知道，在矩阵力学里，乘法中乘的次序很重要，这对应于在后一情形下算符施用于函数的次序很重要。我们会在测不准原理里看到这个问题。

量子理论表达的最后一块基石是关于量子状态的时间演化，总结在第四个假设。

含时薛定谔方程可以通过在经典波动方程中应用量子条件不严格地导出。我们要注意其实在此步骤中没有任何东西得出波动方程的不连续或不确定。在不受外部影响时量子态的演变是完全连续和确定的。然而薛定谔波动方程的含时形式不能描述从一个状态到另一状态的瞬时、不连续和不确定的跃迁。我们称这种跃迁为量子跃迁。玻恩不得不将薛定谔波动力学的确定性方程与玻尔原子理论要求的不确定量子跃迁结合起来论述，纯粹因为后者不能从前者导出。

我们先让子弹飞一会儿。一颗飞行的子弹，在它飞行的时候用一架高速照相机拍照。我们会得到子弹在一系列固定时间上的照片，每一张照片记录了一个特定时刻子弹的位置。通过分析照片序列，我们可以得出子弹的位置，再分别测量子弹的质量，可以计算子弹在飞行方向的动量（质量乘以速度）。假设出于某种好奇心，我们需要计算子弹的位置x和动量p的乘积。选择通过位置乘以动量来计算或者选择动量乘以位置，都不会影响我们想知道的结果。我们称之为经典物理量x和p是可对易的，xp=px。这似乎看来是不言而喻的。但是量子理论的创立者们在1927年发现：对于量子粒子，这些物理量相乘的次序应当有影响。动量p并不是一个独立于位置x的量，它正比于位置变量x关于时间的导数。如果假定xp减px等于ih，其中i是–1的一个平方根，h是约化普朗克常数，理论预测与实验结果就可一致。这称为量子力学位置——动量对易关系。因为h非常小，对于子弹一样的宏观物体的测量不会显示出与我们常识相抵触的行为。而对于微观粒子如电子，就不一样了。然而也正是由于这个案例引人注目，容易用半经典的说法说明，给人留下了刻板的印象，让人们习惯认为量子力学是微观世界里特有的现象。在这本书里我们给出了不太一样的理解，让读者明白量子说的不仅仅涉及微观世界，它描述的系统的关联也会拓展到宏观世界。经典力学可在趋近于零的极限情形下从量子力学恢复出来。

接近量子物理的最直接办法是把原子系统变得低温。德布罗意波长等于普朗克常数除以粒子的动量，而原子的动量跟它的动能成比例，而动能又跟温度成正比。因此，德布罗意波长与温度的平方根成反比，即 。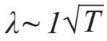

这样物体的温度越低，它的德布罗意波长就越长，其量子特性也越明显。当德布罗意波长这么大尺度的空间里平均只有一个原子的时候，就会发生玻色——爱因斯坦凝聚或者费米狄拉克凝聚（Fermi-Dirac Condensation）。因此为了得到一个足够大（宏观）的量子系统，超冷原子实验的核心问题在于制造一个低温的系统。

熵，出现于热力学第二定律，可能是中学物理很难说清楚的一个概念，因为它的定义涉及微积分的常识，没有相当的数学基础，很难明白它的意义，因此也被“神秘论”所滥用，像其他名词诸如“磁场”和“暗物质”一样。

图2–18 麦克斯韦妖控制隔板上的门，放过这样的分子而把那样的分子拦在门那边(www.xing528.com)

熵，本身代表无序性，熵给了时间的方向。在一个大盒子里放着很多“这样”的分子和“那样”的分子。开始的时候，这样的分子在这边，那样的分子在那边，但所有的分子都不会安静地待着，用不了太久，这样的分子和那样的分子就会混杂在一起。熵，就是说明这个混杂程度的一个物理量。按照热力学第二定律，系统如果是封闭的，它的混乱程度只会增加。也就是说，这样和那样分子再也回不到最初彼此分开的状态了。这时候我们说这样的、那样的分子在盒子里所形成的封闭系统熵增加了。要想让熵减少，需要外界供给能量给这个系统。麦克斯韦提出了一个佯谬，叫作麦克斯韦妖。在盒子中间安一个挡板，把盒子切成两部分。挡板上开个小洞，装一个没有摩擦的小门，派一个小妖看着。当它看见“这样”的分子飞过来，它就打开门，看见“那样”的分子飞过来，它就闭上门。时间足够长之后，这样的和那样的分子就可以再分开了。在这样的和那样的分子、盒子和小妖组成的封闭系统里，熵又可以减少了。麦克斯韦妖的问题困扰了很多科学家。直到香农说：小妖要看到分子飞过来，要分辨是“这样”的分子还是“那样”的分子。做这个判断，是要以处理信息为代价，需要消耗能量的，所以这个系统并不是一个封闭系统。香农也从这一点出发，建立现代信息论，信息处理是一个物理过程，是消耗能量的。

麦克斯韦妖通过观测的方式，从而获得一个比特信息，知道飞过来的分子是这样的还是那样的，决定开门还是关门，把系统的熵降低，付出的代价是耗散kTln2的能量，k是玻尔兹曼常数，ln2是2的自然对数。就是说如果环境温度是T，那么产生一个比特信息就需要付出kTln2焦耳能量为代价。想降低系统的无序程度，要付出耗散热量的代价，这并不违背热力学第二定律定理即熵增加原理。对热力学而言，低温意味着有序化的增加，即熵的减少。如果要达到这样的目的，实验上需要很多很多的麦克斯韦小妖来帮忙区分高速的原子和低速的原子，把低速的原子拣出来，它们的平均温度就降低了。

这里要纠正一个我们习惯上的概念：对称。我们通常说的“对称”，在物理上是不对称的。物理上最大的对称，就是没法分出来哪个方向上或者哪种可能更具有优越性。在上面的例子里，“这样”的分子和“那样”的分子充分混合，是对称的分布，而不是这样的分子在盒子的一边、那样的分子在盒子的另外一边是对称的。玻尔兹曼认识到，如果宇宙是个有限大的封闭整体，没有外界给它能量，那么最终也会完全对称，该发生的反应都发生了，进入一种“热寂”的状态，整个宇宙成了完全没有任何反应的“糨糊”。据说玻尔兹曼因为想到了宇宙的这个终点，深感无聊，决定先走一步。

如果说要让一个系统变得有序，需要外界给它提供能量，这构成一个开放系统。开放系统是可以熵减少的。对称性是可以被破坏的，从而有序化，这是普利高津的对称性自发破缺理论。而正是有了这样的机制，当我们把万有引力考虑进热寂的问题上来时，热寂就不会出现。因为重力的存在，这些弥散在宇宙里的粒子会互相吸引，重新凝聚成这样和那样的分子，组成物质和星球。同时，由于势能提供的能量是负的，它正好充当能量的提供者，因此宇宙这个大系统也可以被看作不封闭的。再远一点，涉及暗物质和暗能量的问题，超出了这本书的讨论范畴，因此我们不再做太多的展开。让系统变得有序化的另外一种方式，我们可以把系统的温度降下来。实验上，我们发展了另外一套办法，从而使系统更容易建立量子的关联。

系统的温度由组成这个系统的分子的随机运动来决定。分子向各个方向无规则运动的平均速度，决定了物体的温度。而让温度降低的办法，可以借助麦克斯韦小妖，一个一个地分辨原子，一个一个来。一个分子系统，把温度降低从而使系统产生关联，向着有序化的方向发展，通过来自一方或几方的简单外力是无法做到的。以这个例子而言，把箱子搬来搬去，或者箱子在外力作用下加速或减速，系统的温度都不会降低，系统也不会变得更有序化。物理上，对应于每一个组成系统的分子，通过跟别的温度更低的分子碰撞，把热量传导带走。但当温度特别低的时候，系统里低温的原子或者分子跟任何容器或介质接触，都只能被加热。这时候物理学家设计了一个巧妙的实验，通过光和原子的能级耦合，让光把原子的能量一个一个一份一份地带走，当然，这个过程要重复很多次。这个过程也可以理解为每一个原子上面住一个麦克斯韦妖，手里拿着一把度量光子能量大小的标尺，这对应于原子的跃迁能级。当光子朝着原子跑过来的时候，小妖判断这个光子是不是能量合适，如果合适就让光子顺便带走一些原子的能量，不合适就直接把光子放走，当作什么都没发生。从信息的角度来讲，这意味着很多信息在被很多小妖分立地独自处理。熵被光子带走，从而获得了整个系统的有序。这个方法，叫作“激光冷却”，获得了1997年的诺贝尔物理学奖。在这样的系统里，光子通过不断地跟原子相互作用，最后原子系统冷却到一个特定的温度，量子关联在系统里所有原子间建立起来，变成为一个肉眼可以见得到的宏观量子体系，我们称之为量子相变——玻色——爱因斯坦凝聚，在原子系统里获得了玻色——爱因斯坦凝聚，获得了2001年的诺贝尔奖。

实验上我们用很多手段，在一个宏观的系统上建立量子体系，量子的宏观体系正不断地突破很多我们常规的认识，量子力学早已不是描述微观的系统。越来越多的实验证实，我们可以在地球上的实验室里制备和研究很大的宏观尺度上的量子行为。更宏观的量子系统，可以在宇宙里的天体找到。我们常常听说的超导就是这样的例子，我们在超导系统里观察到了量子干涉效应。电子是费米子并服从泡利不相容原理，但是把两个自旋配对电子当作单个实体考虑，在适当条件下它们就可以聚合形成玻色子，就有了玻色子的性质，这些电子对可以“凝聚”为玻色——爱因斯坦凝聚态。当大量的电子对在超导体内这样凝聚时，就可以在厘米级甚至更大的尺度上展现出量子的超导效应。电子在这样的超导体内不受阻力。电子间以晶格振动为媒介，形成非常弱的“吸引力”，从而一致行动。这种关联很容易被热运动所克服，因此也需很低的温度，结果一对电子之间的距离可以很大而不需要彼此有电磁力相互作用。因而许多这样的电子对在金属晶格内彼此重叠，电子对所对应的物质波就像激光束中的光波，通过干涉而绕行金属的晶格运动不消耗能量，于是形成超导，不消耗电能没有电阻的导体。人们利用这种宏观量子的干涉效应做各种非常灵敏的器件，比如超导量子干涉器件（sQUID），已经用在医学上临床测量磁场强度的微小变化。利用典型的sQUID，在1秒可检测的最小磁通变化为10-32焦耳，这相当于在地球的引力场里把一个电子举起来一毫米所消耗的能量。超导的电子对可以不在空间域里配对，从而量子的相互作用可以是非局域化的，关联的发生不一定非要发生实际的电磁相互作用。从超导在宏观系统中的实现就可以看出，量子不仅是描述微观世界的工具，它一样在宏观系统中体现，而人类正在不断扩大这一认识。如果把它理解成为一个描述普遍复杂系统关联性质的理论和实验模拟工具，量子系统的关联本性就不再被我们习惯的认识而局限。

读者也许有过这样的经验，站在两面正对的镜子中间。在其中一面镜子里，你看到无数个自己，另外一面镜子里也一样。但事实上，因为眼睛分辨率的限制并且光每次经过镜子反射都会损失一些，所以镜子里人的影像不是无穷多个，人看到自己的影像越来越暗也越来越小直到分辨不出单个的人影。实际上，我们可以用类似的装置来囚禁光子，它也是引力波测量设备的核心部件。

法布里罗伊共振腔是一种可以用来囚禁光子的设备。光学中，法布里——珀罗干涉仪（Fabry-Pérot interferometer）是一种由两块平行的玻璃板组成的干涉仪，其中两块玻璃板相对的内表面都具有高反射率。法布里——珀罗干涉仪也经常称作法布里——珀罗谐振腔（FP腔）。FP腔有个特性，当腔的长度是光半波长的整数倍，光子很容易进入腔里，而一旦腔长不是半波长整数倍，光子进入腔的概率迅速下降。从另一个角度理解，在光子没有进入腔之前，腔之间是真空。真空给出了光可以在腔里稳定待着的所有可能的模式。这就像有很多空的座位，光子需要跟这些座位的尺寸匹配才进得去。进去之后，光在两面镜子之间多次反射，由于镜子里面镀膜很好，反射性质非常优良，光可以被反射几百万次，这时候，光就被囚禁在FP腔里了。

图2–19 经典光学的法布里罗伊共振腔（左）；量子概念的法布里罗伊共振腔（右）

假设光从激光器里射出来，FP腔的长度正好是光半波长的整数倍。当我们减弱光强，直到某一时刻，只有一个光子囚禁在FP腔。这时，我们构建了一个FP腔——光的量子关联系统。如果读者还记得我们讨论的延迟选择实验，我们发现又有一个“因果”的问题。当FP腔长是激光半波长的整数倍，它可以接纳100%的光子的时候，一个光子飞过来，进入光腔，但它怎么知道光腔的长度合适呢？它应该进去跑一趟才知道该不该进去的啊。由于理论上，镜子不能理想地百分之百反射光，光子总有一定的可能从镜子的一侧漏出去，而腔外面是没有边界条件的真空，可以容纳各种各样的模式，光子一旦出去再回到腔里来的概率就非常小。这里我们回顾一下经典意义上由熵发生的时间原因。

宏观上，热力学第二定律即熵增加原理决定了时间的方向，所以又称熵增加理论为“时间之箭”。热的东西变冷，气体在空气中扩散，杯子掉在地上摔碎不会自己拼回来；总之，随着时间的推移，系统会走向更大可能性的状态。熵是描述这种倾向的物理量，最终，系统达到熵最大的状态，我们称之为“热力学平衡”。比如，一杯热咖啡最终会与它所在的房间达到同一温度。如果不进行其他干涉，逆过程是不可能发生的。房间里的咖啡永远不会自发地再次变热，因为热能已经任意地扩散到房间所有的原子上。把这些能量从房间的每个原子那里收集回来并集中到杯子里的原子上，数学上不是不可能，但物理上的可能性太低了，而至于有限的宇宙时间内不可能。

图2–20 经典意义下熵增加的方向决定了时间方向（左）；量子情况下的退相干决定了时间方向（右）

对于量子退相干的过程，光子与腔发生共振，使得腔的某一个振动模式和光子的振动模式耦合而发生量子纠缠。从而光子和腔里的真空形成一个最小的量子相干体系，当光子从腔里逃逸出去，跟真空里所有其他可能的模式都可以相干，与更大空间里的其他物质发生关联的时候，它很难再回到系统中与腔里面的真空发生关联。从这个意义上讲，它跟我们在熵的讨论类似，不是数学上回不去，而是物理上回去的概率太小了。因此，对应于宏观系统里的熵增加，系统因为退相干而导致的关联消失也一样决定了时间的方向。由此我们看到，已认知的世界因为退相干而变成了经典认知的一部分，但经典世界也在不断地重新演化，重新成为量子信息的载体。坍缩被测量，与经典世界相联系，但又立刻重新发生关联而继续演化，这个过程中我们找到了时间的痕迹。