【习题综9.1】如图9.52所示,均质细杆OA质量为m,长为2l,O端用光滑铰链与天花板连接,将杆由水平位置无初速地释放,当杆摆到竖直位置时,O端铰链突然脱落。求铰链脱落后,杆的角速度和杆中心的运动轨迹。
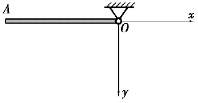
图9.52 习题综9.1图
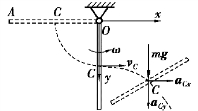
图9.53
【解】从水平到竖直位置的过程中,杆OA绕定轴O转动。
由动能定理有

杆质心(中心)的速度为
![]()
铰链脱落后,杆只在重力作用下作平面运动,其受力及运动分析如图9.53所示。
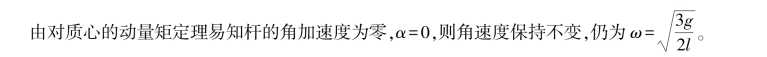
由质心运动定理得
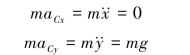
以上微分方程的初始条件分别为
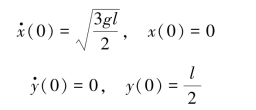
解得质心的运动方程为
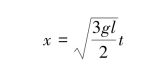
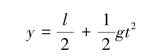
消去时间t得到质心的运动轨迹方程为
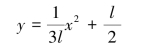
即杆中心的运动轨迹为一抛物线。
【习题综9.2】如图9.54所示,质量为m、半径为r的均质圆轮,受到轻微扰动后,在半径为R的圆弧形轨道上往复滚动。设轨道表面足够粗糙使得圆轮在滚动时无相对滑动,分别运用刚体的平面运动微分方程、功率方程及机械能守恒定律给出圆轮质心C的运动微分方程。
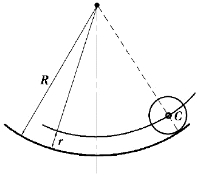
图9.54 习题综9.2图
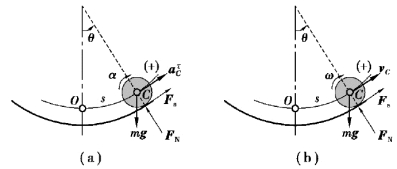
图9.55
【解】方法一:运用刚体平面运动微分方程。
圆轮在圆弧轨道上作平面运动,受到的外力有重力mg,轨道表面的法向约束力FN和摩擦力FS。
设θ角以逆时针为正,取切线轴的正向如图9.55(a)所示,并设圆轮以顺时针转动为正,则图示瞬间刚体运动微分方程在自然轴上的投影式为
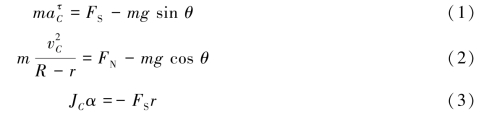
由运动学知,当圆轮只滚不滑时,角加速度的大小为
![]()
取s为质心的弧坐标,由图中几何关系有
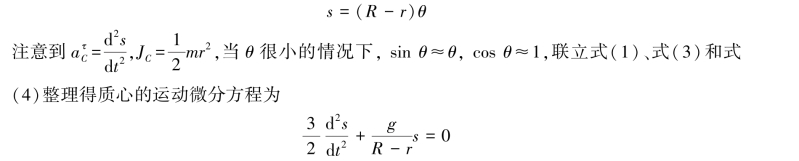
方法二:运用功率方程。
圆轮在圆弧轨道上作平面运动,运动及受力分析如图9.55(b)所示,动能为
![]()
轮与轨道接触点为速度瞬心,接触点的约束力不做功。重力的功率为
![]()

化简得
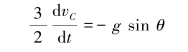
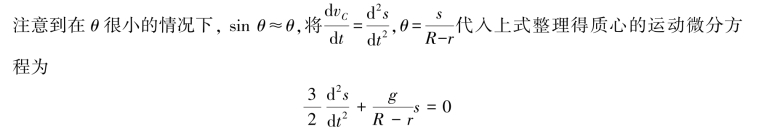
方法三:运用机械能守恒定律。
圆轮在运动过程中,只有重力做功,故机械能守恒。
取质心的最低位置O处为重力势能零点,圆轮在任意位置的势能为
![]()
同一瞬时的动能为
![]()
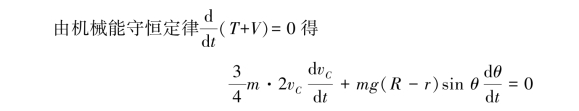
化简得
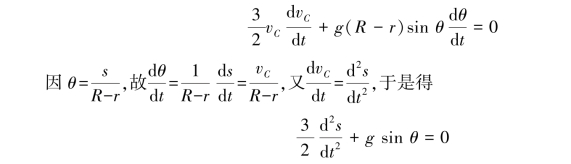
注意到在θ很小的情况下,sinθ≈θ,上式整理得质心的运动微分方程为
![]()
【习题综9.3】如图9.56所示,均质细杆AB质量为m,长为2l,A端用长为l的细绳OA拉住,B端放在光滑水平地面上。初始时,绳OA水平,O、B两点在同一铅垂线上,将系统由静止释放。求当OA运动到竖直位置时,点B的速度以及该瞬时绳子的拉力和地面的约束力。
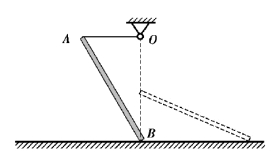
图9.56 习题综9.3图
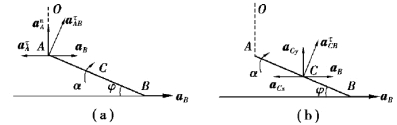
图9.57
【解】首先,求OA运动到竖直位置时点B的速度。
杆由静止释放,初始动能为T1=0。
在竖直位置时,杆瞬时平动,动能为
![]()
在该运动过程中,只有重力做功,有
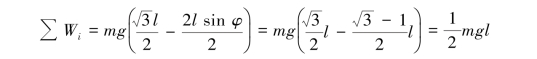
由动能定理T2-T1=∑Wi得
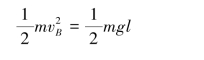
解得
![]()
其次,求绳子的拉力FT和地面约束力FN。
由质心运动定理可列出以下方程

由对质心的动量矩定理可列出以下方程
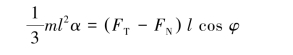
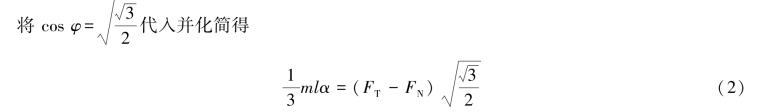
方程(1)和方程(2)有4个未知数,需要补充2个运动学关系。
已知质心C加速度aCy的方向,点A法向加速度anA的大小和方向,点B法向加速度aB的方向。此时,杆AB瞬时平动,ωAB=0。利用平面运动刚体上两点加速度的关系,可列出需要的运动学关系。
以点B为基点,分析点A的加速度如图9.57(a)所示,有
![]()
将其向竖直向上方向投影得
![]()
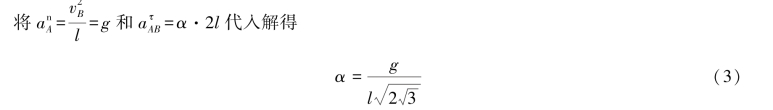
以点B为基点,分析质心C的加速度如图9.57(b)所示,有
![]()
将其向竖直向上方向投影得
![]()
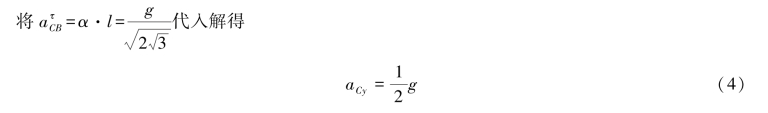
将式(3)和式(4)代入式(1)和式(2),解得
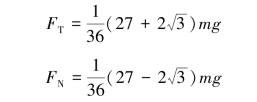
【习题综9.4】如图9.58所示,均质细直杆OA重P=100N,长l=4m,O端为光滑铰链支座,A端用刚度系数k=20N/m的弹簧连于B点,初始杆OA竖直,弹簧处于自然状态。若在杆上施加矩为M=20N·m的力偶,使杆由静止开始转动,求杆转到水平位置时O处支座的约束力。
【解】求杆在水平位置时的约束力,可应用质心运动定理求解,但要先求杆在该位置时质心C的加速度。由于杆OA作定轴转动,故质心的加速度可通过杆的角速度和角加速度计算。角速度可应用动能定理求解,角加速度可由定轴转动刚体的运动微分方程求解。
(1)求杆OA在水平位置时的角速度ω。
杆的动能为
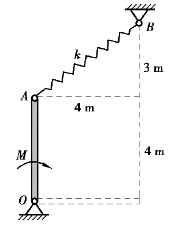
图9.58 习题综9.4图
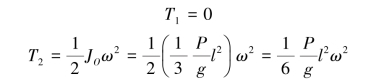
杆在运动过程中,重力、弹性力和力偶做功,所有的力和力偶所做的功为

(2)求杆OA在水平位置时的角加速度α。
杆在水平位置时的受力及运动分析如图9.59所示,此时受到的弹性力大小Fk=kδ=20N/m×2m=40N。由定轴转动刚体的转动微分方程得
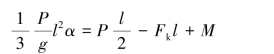
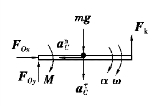
图9.59
将相应数据代入解得此时杆的角加速度为
![]()
(3)求杆OA在水平位置时支座的约束力。
杆在水平位置时,质心加速度为
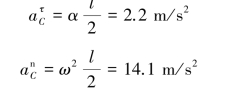
应用质心运动定理得
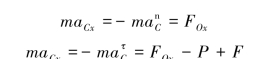
将相应数据代入解得此时支座的约束力为
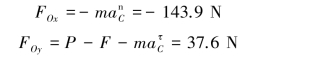
【习题综9.5】如图9.60所示,质量为m、半径为R的薄圆环可绕水平轴O转动。当OC处于水平位置时,圆环由静止开始运动,求运动过程中轴O的约束力与圆环转角φ的关系。若在φ=45°时,轴O突然破坏,求此后圆环的运动。
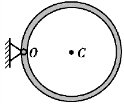
图9.60 习题综9.5图
【解】系统的受力及运动分析如图9.61所示。
首先求圆环转动角速度ω及角加速度α与转角φ的关系。
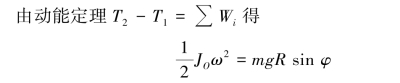
将JO=JC+mR2=2mR2代入整理得
![]()

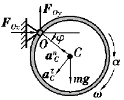
图9.61
根据定轴转动刚体的角速度和角加速度与其上点的加速度之间的关系得
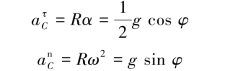
最后求轴O约束力与转角φ的关系。
由质心运动定理得
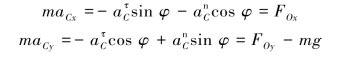
解得
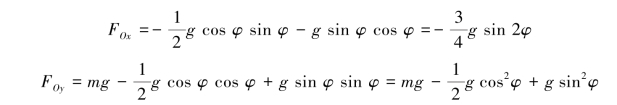
【习题综9.6】如图9.62所示,质量为m1、半径为R的环形管以初角速度ω0绕铅直轴转动,其对铅直轴的转动惯量为J。管内有质量为m2的小球由静止开始自最高处A点开始下落,忽略一切摩擦,求小球到达B处和C处时管的角速度和小球的速度。
【解】研究整体,轴承的约束力都通过转轴,重力平行于转轴,于是有∑Mz(F(e))=0,故系统对转轴z的动量矩守恒。
在初始时刻,小球位于A点,圆环的角速度为ω0,系统对轴z的动量矩为Jω0。小球运动到B点时,设圆环的角速度为ωB,则系统对轴z的动量矩为JωB+m2vBeR=(J+m2R2)ωB(因vBe=RωB)。小球运动到C点时,设圆环的角速度为ωC,则系统对轴z的动量矩为JωC。由动量矩守恒定律得
![]()
于是得
![]()
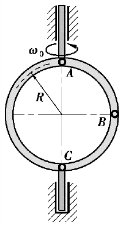
图9.62 习题综9.6图
![]()
因系统在运动过程中,只有小球的重力做功,故系统的机械能守恒。
设小球运动到B点和C点时的速度分别为vB和vC,以初始位置为重力场零势能位置,依题意有
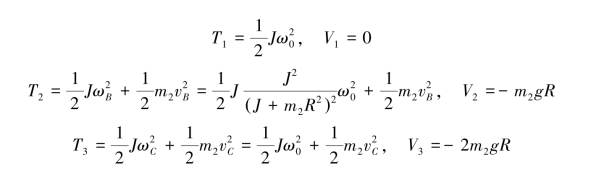
由机械能守恒定律得
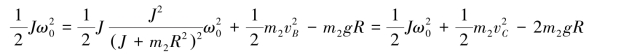
解得
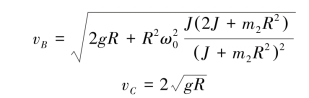
【习题综9.7】如图9.63所示,质量为m1、对中心轴的回转半径为ρ的鼓轮置于摩擦因数为f的粗糙水平面上,并靠在光滑铅垂墙面上。重物A的质量为m2,求重物A的加速度和鼓轮受到的约束力。
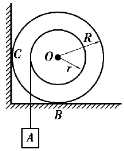
图9.63 习题综9.7图
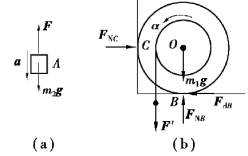
图9.64
【解】重物A直线平动,其受力及运动分析如图9.64(a)所示,运动微分方程为
![]()
鼓轮绕定轴O转动,其受力及运动分析如图9.64(b)所示,运动微分方程为
![]()
由库伦摩擦定律得
![]()
鼓轮转轴过质心,即其质心加速度为零,由质心运动定理易得

补充运动学关系
![]()
联立式(1)—式(6),解得
【习题综9.8】如图9.65所示,质量为m的均质杆AB在两端用两根等长平行的细绳悬挂在天花板上。如果其中一根绳子突然断了,求此瞬间另一绳的张力。
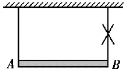
图9.65 习题综9.8图
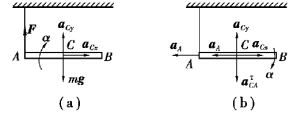
图9.66
【解】初始瞬间,杆的受力及运动分析如图9.66(a)所示,其运动微分方程为

为利用式(1)和式(2)解出绳子的拉力F,需要补充一个运动学关系。初始瞬间杆静止,因点A的速度vA=0,故点A的加速度垂直于绳子即沿水平方向;因角速度ωAB=0,故杆上任意两点的相对加速度的法向分量为零。以点A为基点,分析点C的加速度如图9.66(b)所示,有
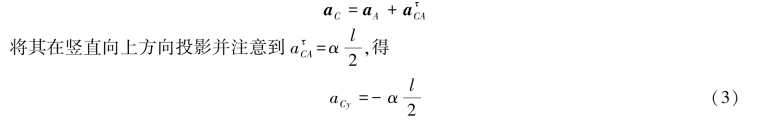
联立式(1)—式(3),解得
【习题综9.9】如图9.67所示,质量为m、半径为r的均质圆柱体,由静止开始自A点沿斜面向下作纯滚动,当它滚到半径为R的圆弧BC上时,求在任意位置上对圆弧轨道的正压力和摩擦力。(已知点A、O和C在同一高度上)
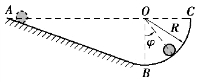
图9.67 习题综9.9图
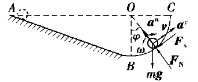
图9.68
【解】研究圆柱体,其运动及受力分析如图9.68所示,由运动学易知v=ωr,由动能定理得
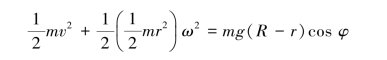
整理得

两边对时间求导并注意到v=(R-r)φ·,可得
![]()
由质心运动定理得
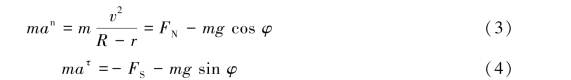
将式(1)和式(2)分别代入式(3)和式(4)解得
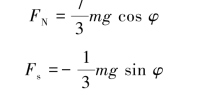
【习题综9.10】如图9.69所示,质量为m、长为l的均质细杆,起初静止紧靠在铅垂墙壁上,由于微小扰动,上端A沿光滑墙面向下滑,下端B沿光滑水平面向右滑。求A端离开墙面前,细杆在任一角度φ时的角速度、角加速度及A和B处的约束力。
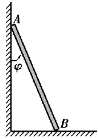
图9.69 习题综9.10图
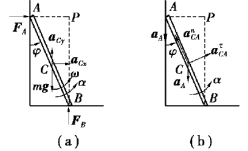
图9.70
【解】研究杆,其受力及运动分析如图9.70(a)所示,P为速度瞬心。
由动能定理得
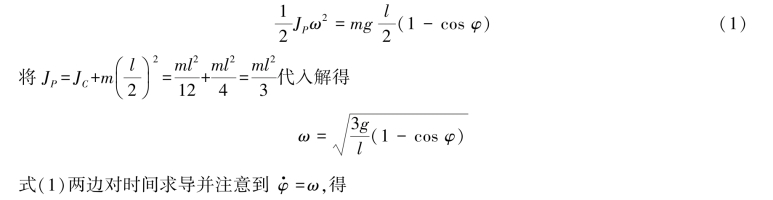
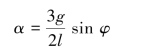
由平面运动刚体的运动微分方程有(https://www.xing528.com)
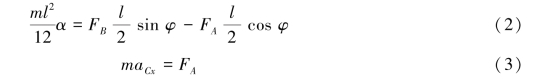
要想利用式(2)和式(3)解得FA和FB,需要求质心加速度在水平向右方向上的投影aCx。为此,以点A为基点,分析质心C的加速度如图9.70(b)所示,有
![]()
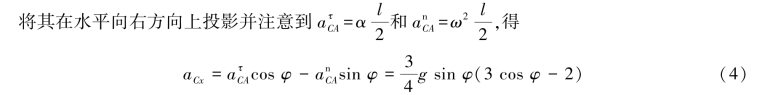
联立式(2)—式(4),解得
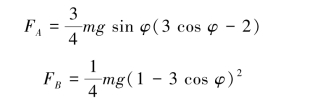
【习题综9.11】如图9.71所示,质量为m、长为l的均质细杆,起初静止紧靠在铅垂墙壁上,由于微小扰动,杆绕B点倒下。不计摩擦,求:(1)B端离开墙面前,细杆在任一角度φ时的角速度、角加速度及B处的约束力;(2)B端离开墙面时的角度φ1;(3)杆着地时质心的速度及杆的角速度。

图9.71 习题综9.11图
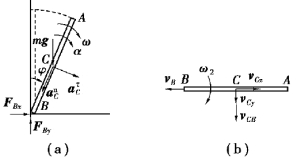
图9.72
【解】(1)未脱离墙时,杆作定轴转动,其受力及运动分析如图9.72(a)所示。由动能定理得
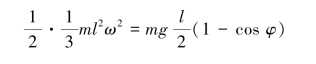
解得
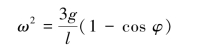
由定轴转动刚体运动微分方程得
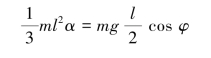
解得
![]()
由质心运动定理得
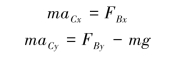
![]()
解得
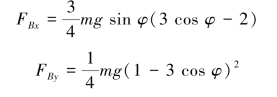
(2)杆脱离墙时有FBx=0,得
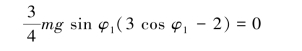
解得
![]()
此时有
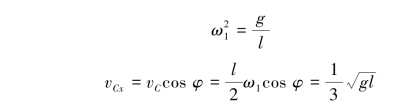
![]()
(3)设杆着地时质心的速度大小为vC,角速度为ω2,研究杆从静止开始到着地时的过程,由动能定理得
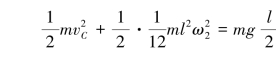

将其在竖直向下方向上投影,注意到vB水平,得
![]()
于是解得
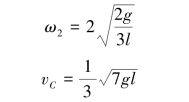
【习题综9.12】如图9.73所示,曲柄滑槽机构中,均质曲柄OA绕水平轴O作匀速转动。已知曲柄OA的质量为m1,长为l;滑槽BD的质量为m2,质心在点C。滑块A的质量和各处摩擦忽略不计。求当曲柄与水平成φ角时,滑槽BD的加速度、轴承O的约束力以及作用在曲柄上的力偶矩M。

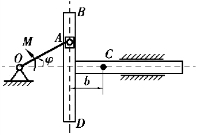
图9.73 习题综9.12图
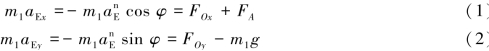
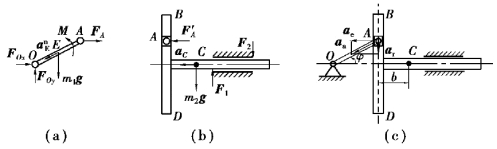
图9.74
由定轴转动刚体的运动微分方程得
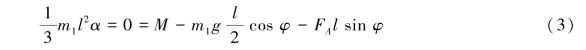
研究滑槽,其受力及运动分析如图9.74(b)所示,由质心运动定理得
![]()
下面求滑槽质心的加速度aC。以杆OA上的A点为动点,动系固定于滑槽,加速度分析如图9.74(c)所示,有
![]()
易得平动滑槽的加速度为
![]()
联立式(1)—式(5)解得
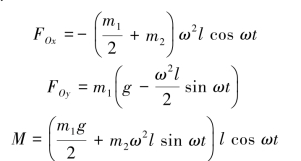
【习题综9.13】如图9.75所示,质量为m1的滚子A沿倾角为θ的斜面向下只滚不滑,用一跨过滑轮B的细绳提升质量为m2的物块C。滚子A和滑轮B质量相等,半径相等,均可视为均质圆盘,求滚子的质心加速度和绳对滚子的拉力。
【解】研究整个系统,任意瞬间其运动分析如图9.76(a)所示,由运动学易知
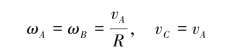
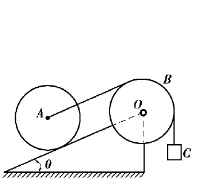
图9.75 习题综9.13图
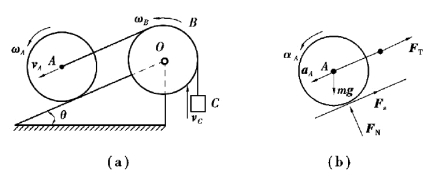
图9.76
则系统的动能为
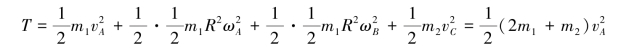
只有滚子和物块的重力做功,系统的功率为
![]()

解得
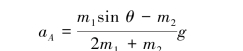
研究滚子A,其受力及运动分析如图9.76(b)所示,易知aA=αAr,由平面运动刚体的运动微分方程得

解得
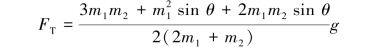
【习题综9.14】如图9.77所示,质量为40kg、边长为100mm的正方形均质等厚板,在铅直平面内用3根细绳拉住。求:(1)绳DE被剪断瞬间,板的加速度以及绳AG和BH的拉力;(2)当绳AG和BH摆到竖直位置时,板的加速度以及两绳的拉力。
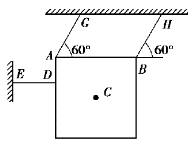
图9.77 习题综9.14图
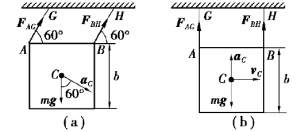
图9.78
【解】(1)剪断绳DE后,板作平面曲线平移。初始瞬间,其受力及运动分析如图9.78(a)所示,质心的加速度aC与绳AG垂直,由平面运动刚体的运动微分方程得
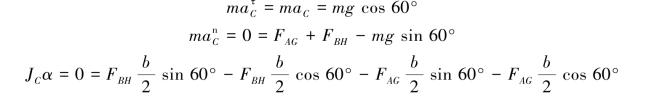
解得
![]()
(2)绳AG和BH摆到竖直位置时,板的受力及运动分析如图9.78(b)所示,设绳长为l,由动能定理得
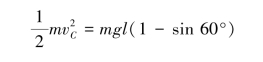
于是得

由平面运动刚体的运动微分方程得
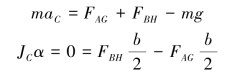
解得
![]()
【习题综9.15】如图9.79所示,三棱柱B沿三棱柱A的斜面滑动,A和B的质量分别为m1和m2,三棱柱A的斜面与水平面成θ角。忽略摩擦,系统由静止开始运动,求三棱柱A的加速度。
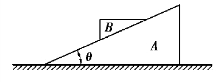
图9.79 习题综9.15图
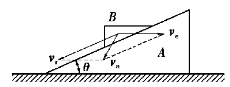
图9.80
【解】三棱柱B的速度分析如图9.80所示,va即为三棱柱B的绝对速度,ve即为三棱柱A的绝对速度,由余弦定理得
![]()
因∑Fx=0,故系统在水平方向动量守恒,又因系统初始静止,则得
![]()
于是得
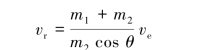
任意时刻,系统的动能为

系统在运动过程中,只有三棱柱B的重力做功,功率为
![]()
式中:φ为m2g与其作用点速度va的夹角。
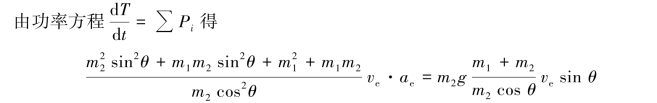
解得三棱柱A的加速度为
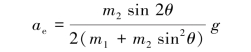
【习题综9.16】如图9.81所示,质量为m1的三棱柱A放在光滑的水平面上。质量为m2的均质圆柱体B由静止沿三棱柱A的斜面向下作纯滚动,设斜面与水平面成θ角。求三棱柱A的加速度。
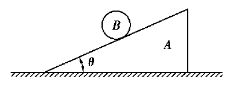
图9.81 习题综9.16图

图9.82
【解】圆柱体质心B的速度分析如图9.82所示,va即为圆柱体质心B的绝对速度,ve即为三棱柱A的绝对速度,由余弦定理得
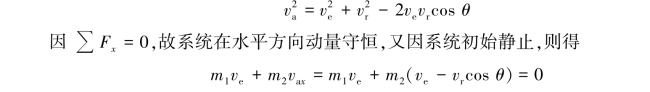
于是得
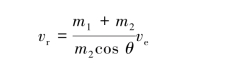
任意时刻,系统的动能为
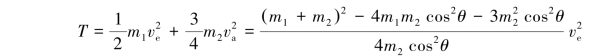
系统在运动过程中,只有圆柱体B的重力做功,功率为
![]()
式中:φ为m2g与其作用点速度va的夹角。
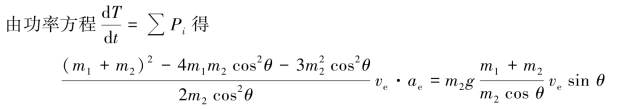
解得三棱柱A的加速度为
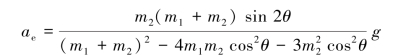
【习题综9.17】如图9.83所示,重为P1,长为l的均质杆AB与重为P的均质三棱柱用光滑铰链B相连,三棱柱置于光滑的水平面上。初始杆AB处于铅垂位置,系统静止。在微小扰动下,杆AB绕铰链B摆动,三棱柱则沿水平面滑动。当杆AB摆至水平位置时,求:(1)杆AB的角加速度;(2)铰链B对杆AB的约束力在铅垂方向的投影大小。
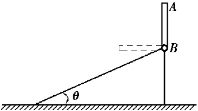
图9.83 习题综9.17图
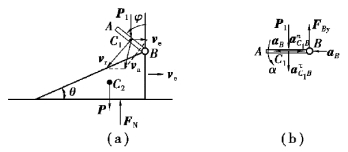
图9.84
【解】(1)任意时刻系统的受力及运动分析如图9.84(a)所示,由运动学易知
![]()
因∑Fx=0,故系统在水平方向动量守恒,又因系统初始静止,则得
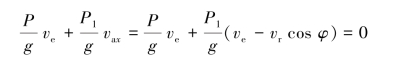
于是得

任意时刻,系统的动能为
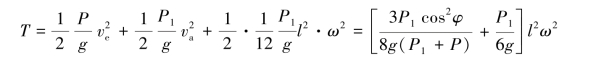
系统在运动过程中,只有杆AB的重力做功,功率为
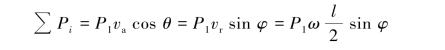
式中:θ为P1与其作用点速度va的夹角。

(2)杆AB水平时铅垂方向的受力分析如图9.84(b)所示,由质心运动定理得
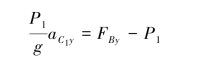
为了求aC1y,以点B为基点,分析杆AB质心C1的加速度如图9.84(b)所示,有
![]()
将其在竖直向上方向投影得
![]()
解得
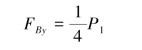
【习题综9.18】如图9.85所示,半径为r的均质圆盘C自桌角O滚离桌面。初始φ=0°,因受微小扰动,均质圆盘由静止开始运动,当φ=30°时,发生滑动现象。求圆盘与桌角间的摩擦因数。
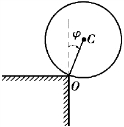
图9.85 习题综9.18图
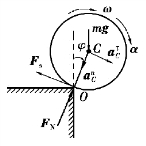
图9.86
【解】圆盘发生滑动之前,作定轴转动。任意时刻,圆盘的受力及运动分析如图9.86所示。
由动能定理得
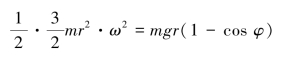
则得

由定轴转动刚体的运动微分方程得
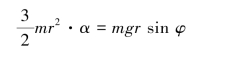
则得
![]()
由质心运动定理得
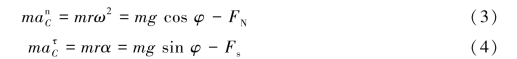
分别将式(1)和式(2)代入式(3)和式(4)解得
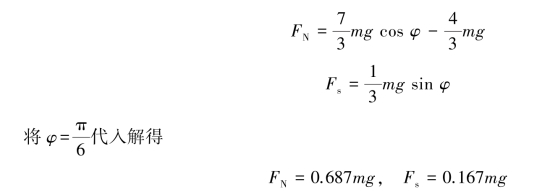
此时,两者应满足库伦摩擦定律,则得
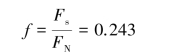
【习题综9.19】如图9.87所示,质量为m、半径为r的均质圆盘放在倾角为30°的斜面上。圆盘与斜面间的动滑动摩擦因数为f。求:(1)平行于斜面的力F应作用在何处,此圆盘才能沿斜面向上滑而不转动;(2)在这种情况下,斜面对圆盘的约束力大小为多少?
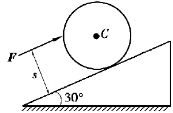
图9.87 习题综9.19图
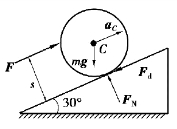
图9.88
【解】假设圆盘沿斜面上滑而不转动,即圆盘平动,其受力及运动分析如图9.88所示,质心aC平行于斜面,角加速度α=0。
在垂直于斜面方向上,由质心运动定理得
![]()
由对质心的动量矩定理得
![]()
由库伦摩擦定律得
![]()
联立式(1)—式(3),解得
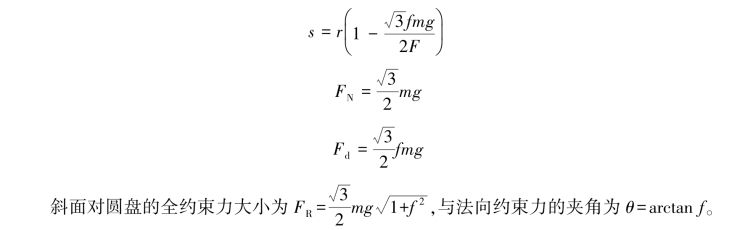
【习题综9.20】如图9.89所示,质量为m、半径为r的均质圆盘从φ=0°的位置静止释放后沿半径为R的导向装置作纯滚动。求圆盘与导轨间的正压力与角φ的关系。
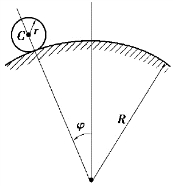
图9.89 习题综9.20图
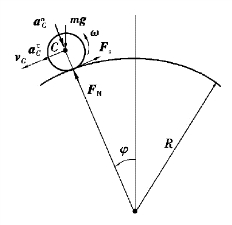
图9.90
【解】圆盘受力及运动分析如图9.90所示。
由动能定理得
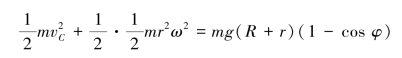
式中rω=vC,整理得
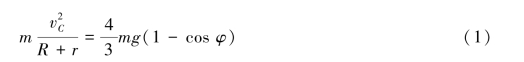
由质心运动定理得
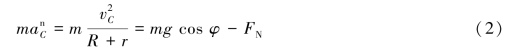
将式(1)代入式(2),解得
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




