【习题8.1】如图8.5所示,小球由不可伸长的绳系住,可绕铅垂轴Oz转动,绳的另一端穿过铅垂小管被力F向下慢慢拉动(不计绳的质量)。开始时小球在M0位置,离Oz轴的距离为R0,小球以转速n0=120r/min绕Oz轴旋转。当小球在M1位置时,R1=R0/2,求此时小球绕O轴转动的转速n1(单位:r/min)。
【解】根据动量矩守恒,有:


图8.5 习题8.1图
解得

【习题8.2】如图8.6所示,通风机叶扇的叶轮的转动惯量为J,以初速度ω0绕其中心轴转动。设空气阻力矩与角速度成正比,方向相反,即M=-αω(α为比例系数),求在阻力作用下,经过多少时间角速度减少一半?在此时间间隔内叶轮转了多少转?
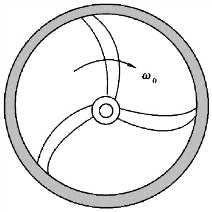
图8.6 习题8.2图

图8.7
【解】以通风机的转动部分为研究对象,其运动受力如图8.7所示,应用动量矩定理得:

分离变量
![]()
将上式积分得:

解得
![]()
再对式(1)积分,将等式左边积分上限改为ω,得
![]()
解得
![]()
即
![]()
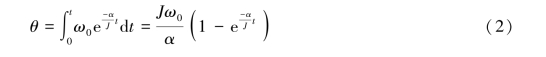

最后得转动部分共转过圈数

【习题8.3】如图8.8所示,水平圆盘可绕铅直轴z转动,其对z轴的转动惯量为Jz。一质量为m的质点在圆盘上作匀速圆周运动,质点的速度为v0,圆的半径为r,圆心到盘中心的距离为l。开始运动时,质点在位置M0,圆盘角速度为零。求圆盘角速度ω与角φ间的关系。
(轴承摩擦不计)
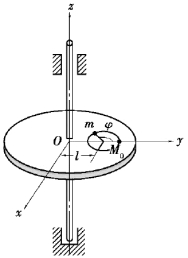
图8.8 习题8.3图
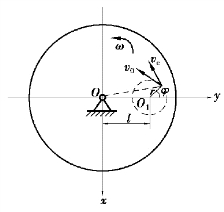
图8.9
【解】以圆板和质点M为系统,因为系统所受外力(包括重力和约束力)对z轴的矩均为零,故系统对z轴的动量矩守恒。在任意时刻点M的速度包含相对速度v0和牵连速度ve。其中
![]()
质点M在M0位置为起始位置,该瞬时系统对轴z的动量矩
![]()
在任意时刻:
![]()
由图8.9可得
![]()
根据动量矩守恒定律,有:
![]()
由式(1)—式(3)得:

【习题8.4】如图8.10所示,图示电绞车提升一质量为m的物体,在其主动轴上作用有一矩为M的主动力偶。已知主动轴和从动轴连同安装在这两轴上的齿轮以及其他附属零件的转动惯量分别为J1和J2;传动比z1∶z2=i;吊索缠绕在鼓轮上,此轮半径为R。设轴承间的摩擦和吊索的质量均略去不计,求重物的加速度。
【解】以主动轴为研究对象,受力如下,应用动量矩定理得:
![]()
以从动轴为研究对象,受力如图8.11(b)所示,应用动量矩定理得:
![]()
以重物为研究对象,受力如图8.11(c)所示,应用牛顿第二定律得:
![]()
注:F和F′,FT和F′T为作用力与反作用力

图8.10 习题8.4图
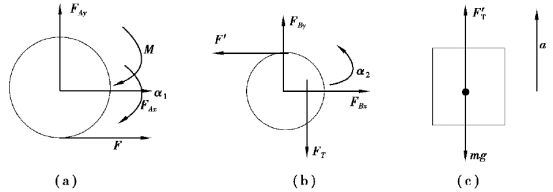
图8.11
再补充运动学关系及结构几何关系方程:


![]()
【习题8.5】如图8.12所示,重物A质量为m1,系在绳子上,绳子跨过不计质量的固定滑轮D,并绕在鼓轮B上。由于重物下降,带动了轮C,使它沿水平轨道滚动而不滑动。设鼓轮半径为r,轮C的半径为R,两者固连在一起,总质量为m2,对于其水平轴O的回转半径为ρ。求重物A的加速度。

图8.12 习题8.5图

图8.13
【解】分别取重物A和鼓轮B为研究对象,其受力和运动分析如图8.13(a)、8.13(b)所示。重物A的运动微分方程为
![]()
轮B作平面运动,其运动微分方程为

由于轮子只滚不滑,故有

联立式(1)—式(5)求解,得

【习题8.6】如图8.14所示,两带轮的半径各为R1和R2,其质量各为m1和m2,两轮以胶带相连接,各绕两平行的固定轴转动。如在第一个带轮上作用矩为M的主动力偶,在第二个带轮上作用矩为M′的阻力偶。带轮可视为均质圆盘,胶带与轮间无滑动,胶带质量略去不计。求第一个带轮的角加速度。
【解】对1轮应用动量矩定理得:
![]()
对2轮应用动量矩定理得:
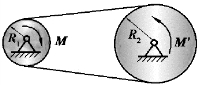
图8.14 习题8.6图

由

解得:
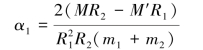
【习题8.7】如图8.15所示,为了求得半径R=50cm的飞轮A对于通过其重心O的轴的转动惯量,在飞轮上系一细绳。绳的末端系一质量m1=8kg的重锤,重锤自高度h=2m处落下,测得落下时间T1=16s。为了消去轴承摩擦的影响,再用质量m2=4kg的重锤做第二次试验,此重锤自同一高度落下来的时间是T2=25s。假定摩擦力矩为一常量,且与重锤的质量无关,试计算转动惯量J。
【解】取飞轮A及重物为质点系,设摩阻力偶矩为Mf,飞轮转动惯量为JA,如图8.16所示。根据对轴A的投影式动量矩定理有:

图8.15 习题8.7图
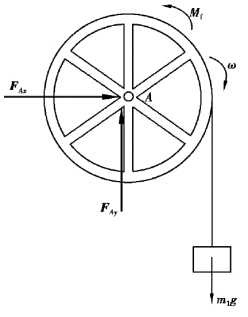
图8.16
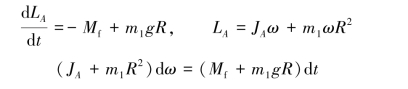
两边积分得
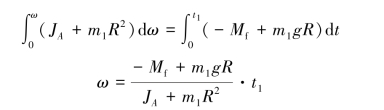

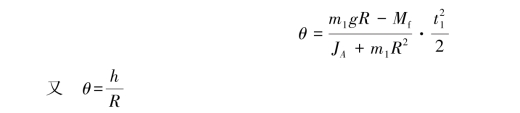
故

将第1次试验时的m1、t1替换为第2次试验时的m2、t2,得

联立式(1)、式(2),解得:
![]()
【习题8.8】为求刚体对于通过重心G的轴AB的转动惯量,用两杆AD、BE与刚件牢固连接,并借两杆将刚体活动地挂在水平轴DE上,如图8.17所示。轴AB平行于DE,然后使刚体绕轴DE作微小摆动,求出振动周期T。如果刚体的质量为m,轴AB与DE间的距离为h,杆AD和BE的质量忽略不计,求刚体对轴AB的转动惯量。

图8.17 习题8.8图

图8.18
【解】取刚体系统为研究对象,如图8.18所示。设刚体离开平衡位置转过一微小角度θ,由刚体绕定轴转动的微分方程式有:
![]()
由于θ很小,有
得该系统自由振动的周期为:
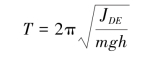

![]()
由刚体转动惯量的平行移轴定理有
![]()
将JDE值代入上式解得:
![]()
【习题8.9】如图8.19所示,均质圆盘的半径R=180mm,质量m=25kg。测得圆盘的扭转振动周期T1=1s;当加上另一物体时,测得扭转振动周期为T2=1.2s。求所加物体对于转动轴的转动惯量。
【解】
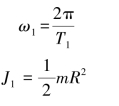
加上另一物体的前后,由动量守恒得:

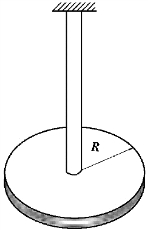
图8.19 习题8.9图
【习题8.10】两匀质细杆OA和EC的质量分别为50kg和100kg,在A点被互相垂直焊接。若此结构在图示位置由静止释放,求释放瞬时,铰支座O的约束力和杆OA作用于杆EC的弯矩。(尺寸如图8.20所示,不计铰的摩擦)
【解】T形结构对O点应用动量矩定理:

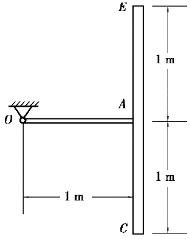
图8.20 习题8.10图
应用质心运动定理:
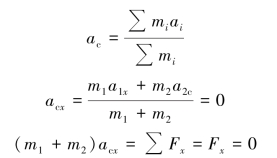
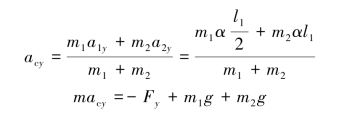
联立上式解得:
![]()
对质心运用动量矩定理:
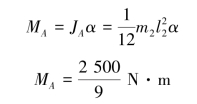
【习题8.11】如图8.21所示,均质杆AB长为l,质量为m1。杆的B端固连质量为m2的小球,其大小不计。杆上点D连一弹簧,刚度系数为k,使杆在水平位置保持平衡。设初始静止,求给小球B一个垂直向下的微小初位移δ0后杆AB的运动规律和周期。
(1)以AB杆和球为研究对象,受力如图8.22所示。
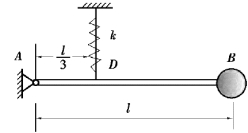
图8.21 习题8.11图

图8.22 习题8.11图
(2)运动分析:AB杆和球绕A点定轴转动,转角为φ,顺时针为正,并取弹簧静平衡位置为φ的坐标原点。
(3)由刚体定轴转动微分方程得:(https://www.xing528.com)

【习题8.12】如图8.23所示,有一轮子,轴的直径为50mm,无初速地沿倾角θ=20°的轨道滚下(设只滚不滑),5s内轮心滚过距离s=3m。试求轮子对轮心的回转半径。

图8.23 习题8.12图
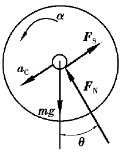
图8.24
【解】取轮子为研究对象,轮子受力如图8.24所示,根据刚体平面运动微分方程有:
![]()
因轮子只滚不滑,所以有
![]()
将式(3)代入式(1)和式(2),消去F得
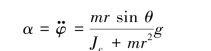
对时间2次积分,并注意到t=0时φ=0,φ·=0,则有
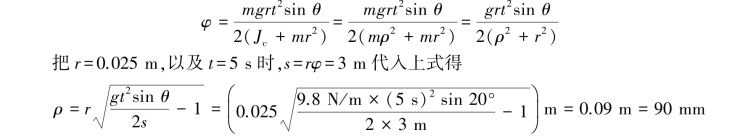
【习题8.13】如图8.25所示均质杆AB长为l,放在铅直平面内,杆的一端A靠在光滑的铅直墙上,另一端B放在光滑的水平地板上,并与水平面成φ0角。此后,令杆由静止状态倒
下。求:(1)杆在任意位置时的角加速度和角速度;(2)当杆脱离墙时,此杆与水平面的夹角。

图8.25 习题8.13图
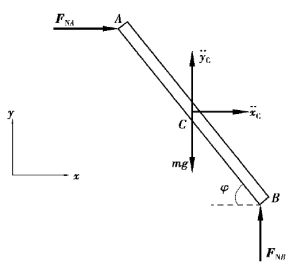
图8.26
【解】(1)取均质杆为研究对象,受力及坐标系Oxy如图8.26所示。杆AB作平面运动,质心在点C。刚体平面运动微分方程为

得

将式(4)、式(5)代入式(1)和式(2),得
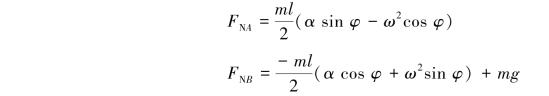
再将FNA,FNB的表达式代入式(3)中,得

分离变量并积分得

(2)当杆脱离墙体时,FNA=0,设此时φ=φ1,则有
![]()
将α和ω的表达式代入上式解得

【解】取均质圆柱为研究对象,受力如图8.28所示。圆柱作平面运动,其平面运动微分方程为

图8.27 习题8.14图

图8.28

且
![]()
圆柱沿斜面向下滑动,可看成沿绳AD向下滚动,且只滚不滑,所以有

联立式(1)—式(5),解得:aC=0.355g(方向沿斜面向下)。
【习题8.15】均质圆柱体A和B的质量均为m,半径为r,一绳缠在绕固定轴O转动的圆柱A上,绳的另一端绕在圆柱B上,如图8.29所示。摩擦不计,求:(1)圆柱体B下落时质心的加速度;(2)若在圆柱体A上作用一逆时针转向、矩为M的力偶,试问在什么条件下圆柱体B的质心加速度的方向向上。
【解】(1)分别取轮A和B研究,其受力如图8.30所示。轮A定轴转动,轮B作平面运动。
对轮A运用刚体绕定轴转动的微分方程,有:
![]()

图8.29 习题8.15图
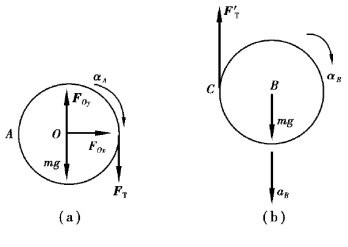
图8.30
对轮B运用刚体平面运动的微分方程,有:

再以C为基点分析点B加速度,有

联立式(1)—式(4)联立,解得

(2)若在轮A上作用1逆时针转矩M,则轮A将作逆时针转动,对A运用刚体绕定轴转动微分方程有:

以点C为基点,分析点B的加速度。根据题意,在临界状态有
![]()
联立式(5)、式(6)、式(2)、式(3),解得:
![]()
故当转矩M>2mgr时,轮B的质心加速度将向上。
【习题8.16】如图8.31所示,均质梁AB长l,重W,由铰链A和绳所支持。若突然剪断联结B点的软绳,求绳断前后铰链A的约束力的改变量。

图8.31 习题8.16图
【解】以梁AB为研究对象,在绳断瞬间应用动量矩定理,有

求得
![]()
梁AB质心点C的加速度为
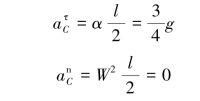
求得
![]()
剪断前
![]()
故铰链的约束力的改变量为:
![]()
【习题8.17】圆轮A的半径为R,与其固连的轮轴半径为r,两者的重力共为W,对质心C的回转半径为R,缠绕在轮轴上的软绳水平地固定于点D。均质平板BE质量为m,可在光滑水平面上滑动,板与圆轮间无相对滑动。若在平板上作用一水平力F,试求平板BE的加速度。
【解】对轮C作受力图如下
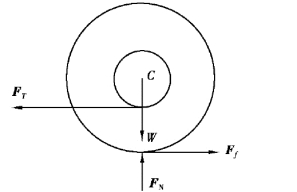
对C点运用动量矩定理,
![]()
其中
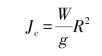
对C质心水平方程运用动量定理
![]()
补充运动方程:
![]()
对板BE,作受力图如下
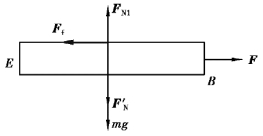
有
![]()
补充运动方程
![]()
取立式(1)—式(5),求得
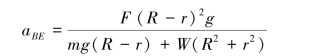
【习题8.18】图示重物A的质量为m,当其下降时,借无重且不可伸长的绳使滚子C沿水平轨道滚动而不滑动。绳子跨过不计质量的定滑轮D并绕在滑轮B上。滑轮B与滚子C固结为一体。已知滑轮B的半径为R,滚子C的半径为r,二者总质量为m′,其对与图面垂直轴O的回转半径为ρ。求:重物A的加速度。
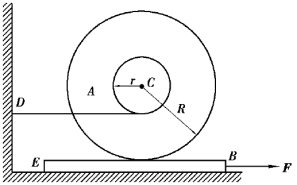
图8.32 习题8.17图
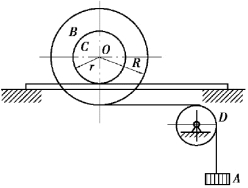
图8.33 习题8.18图
【解】分别取重物A和鼓轮B为研究对象,其受力和运动分析如图8.34(a)、(b)所示。
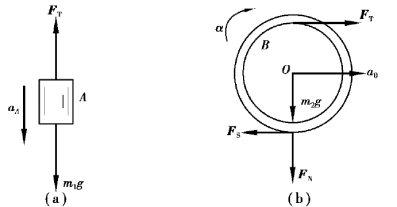
图8.34
重物A的运动微分方程为
![]()
轮B作平面运动,其运动微分方程为
![]()
由于轮子只滑不滚,故有

联立式(1)—式(5)求解,得

【习题8.19】鼓轮如图8.35所示,其外、内半径分别为R和r,质量为m,对质心轴O的回转半径为ρ,且ρ2=R·r,鼓轮在拉力F的作用下沿倾角为θ的斜面往上作纯滚动。F力与斜面平行,不计滚动摩阻,试求质心O的加速度。
【解】作运动受力图如图8.36所示,对鼓轮应用质心动量矩定理

图8.35 习题8.19图
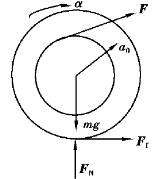
图8.36
![]()
质心动量定理
![]()
补充运动学关系方程
![]()
联立式(1)—式(3)并考虑到J0=mρ2=mRr,求得
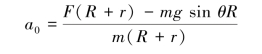
【习题8.20】如图8.37所示,圆柱体A的质量为m,在其中部绕以细绳,绳的一端B固定。圆柱体沿绳子解开而降落,其初速为零。求当圆柱体的轴降落了高度h时圆柱体中心A的速度v和绳子的拉力FT。
【解】圆柱体作平面运动,受力分析如图8.38所示。应用平面运动微分方程(y为竖直向下坐标),有

圆柱体绕绳切点纯滚动,补充运动学方程
![]()
联立式(1)—(3),求得
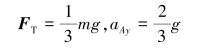
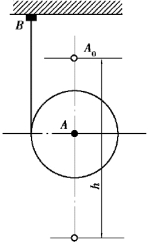
图8.37 习题8.20图
圆柱体质心为竖直向下匀加速运动,故有
![]()
即下降h时,圆柱体耗时
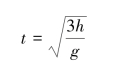
此时,质心A的速度


图8.38
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




