理论力学综合训练习题详解

【习题综6.1】如图6.54所示结构由杆AB及弯杆

DB组成，P＝10N，M＝20N·m，L＝r＝1m，各杆及轮自重不计，求固定支座A及滚动支座D的约束反力及杆BD的B端所受的力。

【解】（1）取整体为研究对象，受力分析如图6.55（a）所示。

列平衡方程：

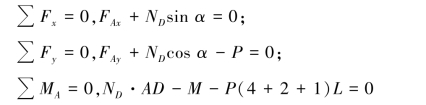
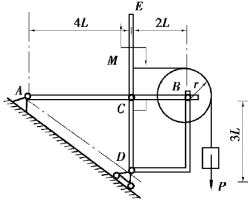
图6.54　习题综6.1图

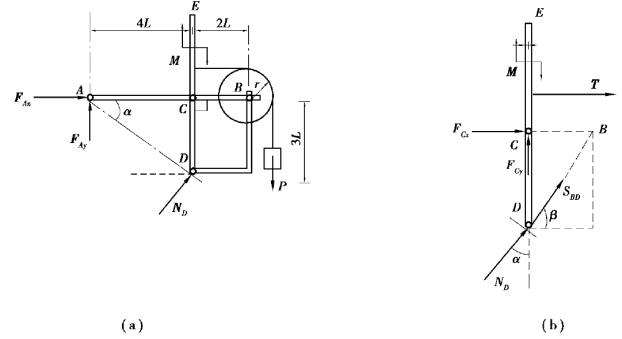
图6.55

因为AC＝4L，CD＝3L，L＝1

所以AD＝5

所以ND＝18N，FAx＝－10.8N，FAy＝－4.4N（与图示方向相反）

（2）由于BD杆为二力构件，SBD＝SDB

取DE杆为研究对象，受力分析如图6.55（b）所示。

列平衡方程：

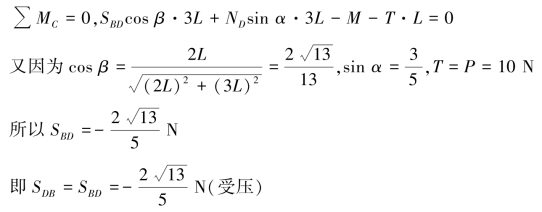
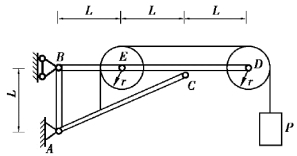
图6.56　习题综6.2图

【习题综6.2】重为P的重物按图示方式挂在三角架上，各杆和轮的自重不计，尺寸如图6.56所示，试求支座A、B的约束反力及AB杆内力。

【解】（1）取整体为研究对象，受力分析如图6.57（a）所示。

列平衡方程：

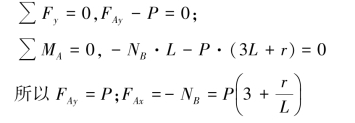
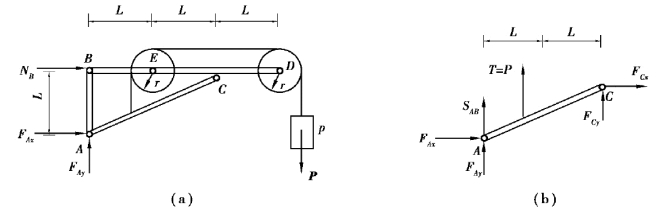
图6.57

（2）由于AB杆为二力杆，SAB＝SBA，取AC杆为研究对象，受力分析如图6.57（b）所示。列平衡方程：

解得：SAB＝0

【习题综6.3】构架如图6.58所示，重物Q＝100N，悬挂在绳端。已知：滑轮半径R＝10cm，L1＝30cm，L2＝40cm，不计各杆及滑轮、绳的质量，试求A、E支座反力及AB杆在铰链D处所受的力。

【解】（1）取整体为研究对象，由于EC杆为二力杆，整体受力分析如图6.59（a）所示。

列平衡方程：

∑MA＝0，FE·L2－Q·（2L1＋L1＋R）＝0，

所以FEx×0.4－100×（3×0.3＋0.1）＝0

所以FEx＝250N

∑Fx＝0，FAx－FE＝0；

∑Fy＝0，FAy－P＝0；

所以FAx＝250N；FAy＝100N

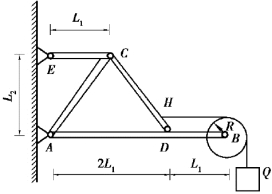
图6.58　习题综6.3图

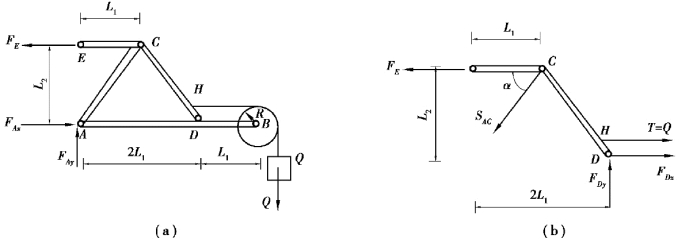
图6.59

（2）取ECHD为研究对象，受力分析如图6.59（b）所示。

列平衡方程：

∑Fx＝0，FDx＋T－FE－SACcosα＝0；

∑Fy＝0，FDy－SACsinα＝0；

∑MD＝0，FE·L2－TR＋SACcosα·L2＋SACsinα·L1＝0

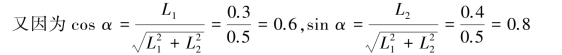
所以SAC＝189.5N，FDx＝37.5N，FDy＝－150N

【习题综6.4】重P、半径为r的均质圆轮沿倾角为θ的斜面向下滚动，如图6.60所示。求轮心C的加速度，并求圆轮不滑动的最小摩擦系数。

【解】以圆轮为研究对象，受力如图6.61所示。

圆轮作平面运动，轮心作直线运动，则aC＝rα。

将惯性力系向质心简化，惯性力和惯性力偶矩的大小为

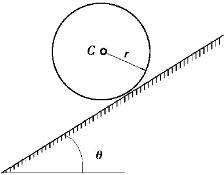
图6.60　习题综6.4图

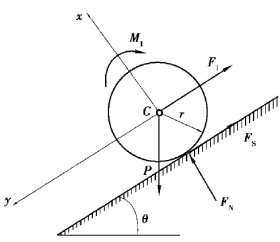
图6.61

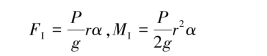
则由质点系的达朗贝尔原理，有：

∑Fx＝0，FN－Pcosθ＝0；

∑Fy＝0，Psinθ－FS－FI＝0；

∑MC＝0，FSr－MI＝0

【习题综6.5】如图6.62所示，已知两均质直杆自水平位置无初速地释放。求两杆的角加速度和O、A处的约束反力。

图6.62　习题综6.5图

【解】（1）取系统为研究对象，受力如图6.63（a）所示。(www.xing528.com)

图6.63

惯性力和惯性力偶矩的大小分别为：

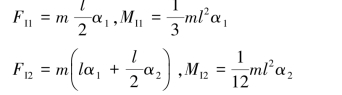
对整体列平衡方程：

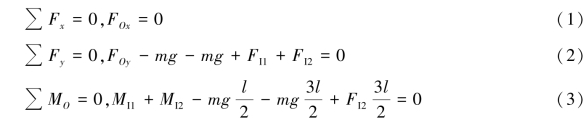
（2）取AB杆为研究对象，受力如图6.63（b）所示。

列平衡方程：

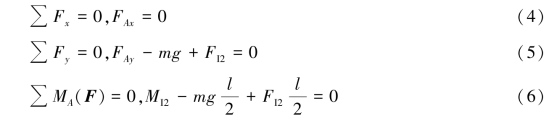
联立方程（1）—方程（6）解得：

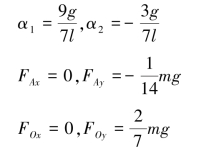
【习题综6.6】均质杆的质量为m，长为2l，一端放在光滑地面上，并用两软绳支持，如图6.64所示。求当BD绳切断的瞬时，B点的加速度、AE绳的拉力及地面的反力。

【解】以AB杆为研究对象，杆AB作平面运动，加速度分析如图6.65（a）所示。

以B点为基点，则C点的加速度为

其中

在BD绳切断的瞬时，受力如图6.65（b）所示。

由质点系的达朗贝尔原理，有：

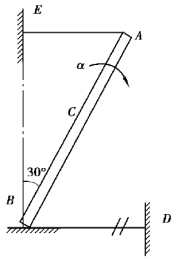
图6.64　习题综6.6图

图6.65

即

即

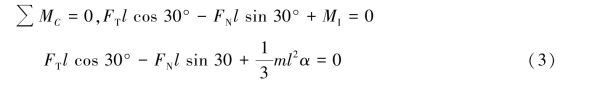
以B为基点，分析A点加速度如图6.65（c）所示。

A点的加速度为

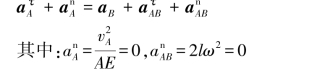
将上式投影到水平方向，得

联立求解式（1）—式（4），得：

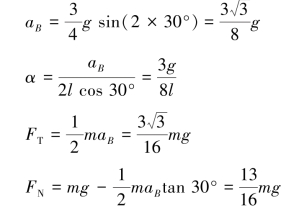
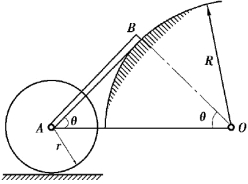
图6.66　习题综6.7图

【习题综6.7】如图6.66所示，均质杆AB长为l，重为Q，上端B靠在半径为R的光滑圆弧上（R＝l），下端A以铰链和均质圆轮中心A相连，圆轮重P，半径为r，放在粗糙的地面上，由静止开始滚动而不滑动。若运动开始瞬时杆与水平线所成夹角θ＝45°，求此瞬时A点的加速度。

【解】设系统运动的初瞬时，圆轮中心的加速度为aA，角加速度为εA；AB杆的角加速度为ε，质心C的加速度为aCx、aCy，如图6.67（a）所示。

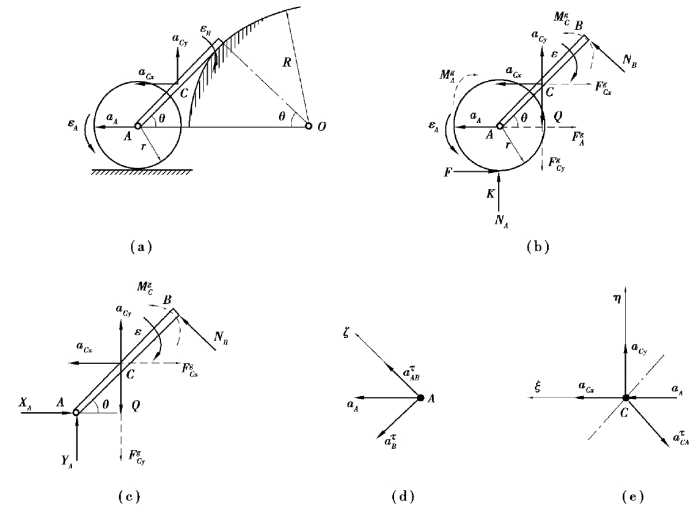
图6.67

轮和杆均作平面运动，将惯性力系分别向质心简化，则惯性力和惯性力偶的矩的大小分别为：

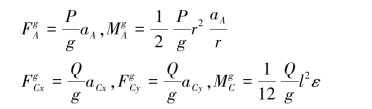
先以整体为研究对象，假想地加上惯性力和惯性力偶，受力分析如图6.67（b）所示。

由质点系的达朗贝尔原理得：

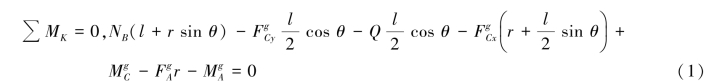
再以AB为研究对象，假想的加上惯性力和惯性力偶，受力如图6.67（c）所示。

则由质点系的达朗贝尔原理得：

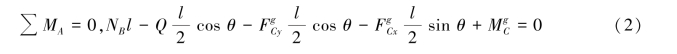
AB杆作平面运动，先以B点为基点，则A点的加速度为

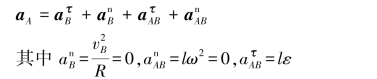
则A点的加速度合成矢量图如图6.67（d）所示。将其投影于ξ轴，得：

再以A为基点，则C点的加速度为：

将其投影于ξ和η轴，得：

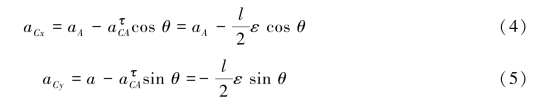
由式（3）—式（5）可将ε，aCx，aCy都化为aA的函数，即

将其代入式（1）、式（2），并取θ＝45°，联立该两方程可解得：