
【解】以点A为基点,将圆柱的平面运动分解为随基点A的平移和绕基点A的转动。
先求基点A的方程。坐标系中

图3.3 习题3.1图
![]()
改写成
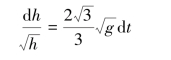
上式积分
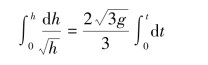
得
![]()
依题意,有
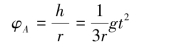
故圆柱的平面运动方程为

【习题3.2】杆AB的A端沿水平线以等速v运动,运动时杆恒与一半径为R的半圆周相切,如图3.4所示。如杆与水平线间的夹角为θ,以角θ表示杆的角速度。
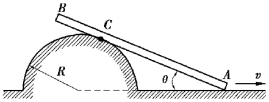
图3.4 习题3.2图

图3.5
【解】如图3.5所示,杆AB做平面运动,A点速度沿水平方向,C点速度沿半圆周切线方向。以A为基点,点C速度分析可得

【习题3.3】如图3.6所示,两平行条沿相同的方向运动,速度大小不同,v1=6m/s,v2=2m/s。齿条之间夹有一半径r=0.5m的齿轮,试求齿轮的角速度及其中心O的速度。

图3.6 习题3.3图
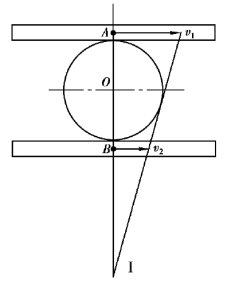
图3.7
【解】运动分析如图3.7所示,由瞬心法(I为瞬心),有

【习题3.4】如图3.8所示为四连杆机构,连杆AB上固连一块三角板ABD。机构由曲柄O1A带动。已知:曲柄的角速度ω01A=2rad/s;曲柄O1A=0.1m,水平距离O1O2=0.05m,AD=0.05m;当O1A⊥O1O2时,AB平行于O1O2,且AD与AO1在同一直线上,角φ=30°,求三角板ABD的角速度和点D的速度。

图3.8 习题3.4图

图3.9
【解】三角板ABD作平面运动,在图3.9所示位置,速度瞬心在点P,设三角板角速度为ωAB,有:

则
![]()
【习题3.5】如图3.10所示平面机构中,AB=BD=DE=l=300mm。在图示位置时,BD∥AE杆AB的角速度为ω=5rad/s。试求此瞬时杆DE的角速度和杆BD中点C的速度。

图3.10 习题3.5图
【解】(1)求杆DE的角速度。杆BD作平面运动,vB的大小为vB=ωl=1.5m/s,方向与AB垂直。
以B点为基点,应用速度合成定理,D点的速度可表示为
![]()
其中,D点绕B的转动速度vDB的方向与BD垂直,D点的速度vD与DE垂直。
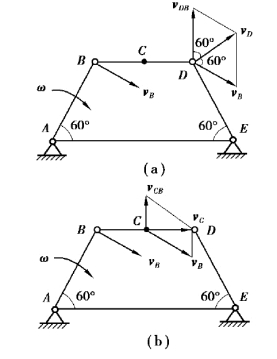
图3.11
由速度合成矢量图(图3.11)可得:

(2)求杆BD中点C的速度。仍以B点为基点,C点的速度可表示为
![]()
其中vB大小和方向均为已知,vCB方向为BD杆垂直,大小为
![]()
由此瞬时速度矢的几何关系,得出此时vC的方向恰好沿杆BD,大小为
![]()
【习题3.6】曲柄滑块机构如图3.12所示,曲柄OA以匀角速度ω转动。已知曲柄OA长为R,连杆AB长为l。当曲柄在任意位置φ=ωt时,求滑块B的速度。

图3.12 习题3.6图

图3.13
【解】(1)基点法。因为A点速度vA已知,故选A为基点。应用速度合成定理,B点的速度可表示为vB=vA+vBA,其中vA的大小为vA=Rω,由速度合成矢量图(图3.13)可得:

![]()
因此可求得连杆AB的角速度为

(2)速度投影法。应用速度投影定理(图3.14),有
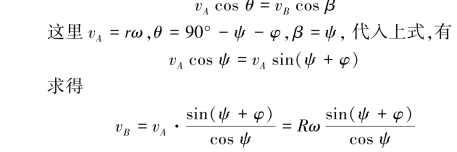

图3.14


图3.15 习题3.7图

图3.16
【解】由速度投影定理,杆AB上A,B点的速度在AB线上投影相等,即
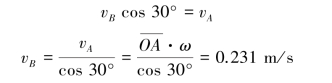
摇杆CD绕C点作定轴转动

轮E沿水平面滚动,轮心E的速度沿水平方向,由速度投影定理,D、E两点的速度关系为
![]()
求得
![]()

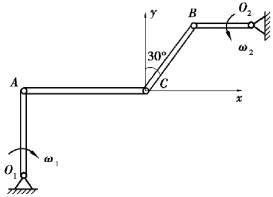
图3.17 习题3.8图

图3.18
【解】先求出A点和B点的速度,有

以A点为基点分析C点的速度,有
![]()

把vC=vB+vCB式分别投影到x,y轴上,得:

得:



图3.19 习题3.9图

图3.20
【解】连杆AB作平面运动,其他构件作定轴转动,vA⊥O1A,vB⊥OB,故连杆AB的速度瞬心在AO1和BO延长线的交点P(图3.20)。设轮Ⅰ与轮Ⅱ的啮合点为C。此时△ABP为直角三角形,γ=60°,由几何关系知:
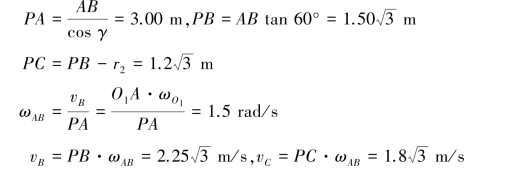
曲柄OB的角速度

齿轮Ⅰ的角速度

【习题3.10】如图3.21所示机构中,矩形板用两根长0.15m的连杆悬挂,已知图示瞬时连杆AB的角速度为4rad/s,其方向为顺时针。试求:(1)板的角速度;(2)板中心G的速度;(3)板上F点的速度;(4)找出板中速度等于或小于0.15m/s的点。

图3.21 习题3.10图

图3.22
【解】(1)求板的角速度。如图3.22所示,板BDHF的瞬心在I点处,BI=BD=ID=0.2m,

(2)求板中心G的速度
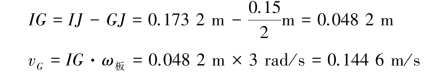
(3)求板上F点的速度

(4)求板中速度等于或小于0.15m/s的点
![]()
板中速度等于或小于0.15m/s的点在以瞬心I为圆心,半径为0.05m的圆内,圆周上速度为0.15m/s,圆内速度小于0.15m/s。

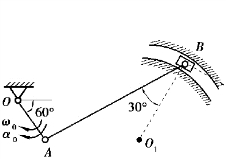
图3.23 习题3.11图
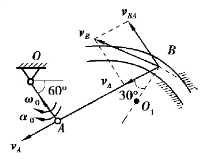
图3.24
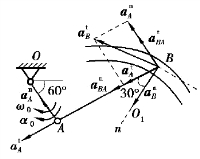
图3.25
【解】曲柄OA上点A的速度和加速度为
![]()
以点A为基点分析杆AB上点B的速度与加速度,则点B的速度为

分别向轴n,轴t投影,得
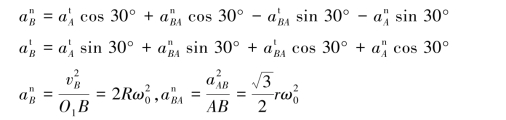
代入式(1),可解得
![]()
因此滑块B的加速度为

【习题3.12】滚压机构的滚子沿水平面滚动而不滑动,已知曲柄OA长r=10cm,以匀转速n=30r/min转动。连杆AB长l=17.3cm,滚子半径R=10cm。求在图示位置时滚子的角速度及角加速度。
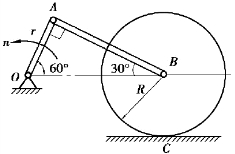
图3.26 习题3.12图

图3.27
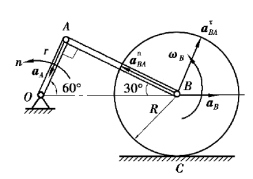
图3.28
【解】vA=ωr,连杆AB做平面运动,由速度投影定理:vA=vBcos30°,滚子做纯滚动,则


其中:
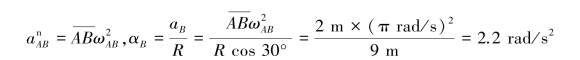


图3.29 习题3.13图

图3.30(https://www.xing528.com)
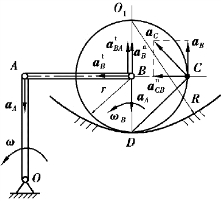
图3.31
【解】(1)速度分析。AB杆瞬时平移,有:
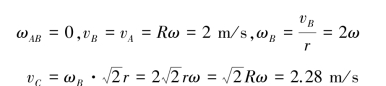

将上式向AB方向投影,得

以B为基点,则有

【习题3.14】半径为R的轮子沿水平面滚动而不滑动,如图3.32所示。在轮上有圆柱部分,其半径为r。将线绕于圆柱上,线的B端以速度v和加速度a沿水平方向运动。求轮的轴心O的速度和加速度。
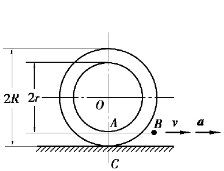
图3.32 习题3.14图
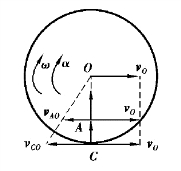
图3.33
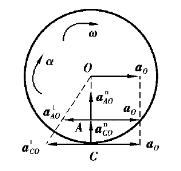
图3.34
【解】因轮子沿水平面滚动而不滑动,所以轮上与地面接触点C的速度为0,且轮上C点的加速度沿水平方向的投影也为0。以轮心O为基点分析轮上点A及点C的运动。设轮心O的速度为vO,加速度为aO,则有
![]()
设轮子滚动的角速度为ω,角加速度为α,则有


将上式向水平轴投影,得
![]()
由于
![]()
故可解得
![]()
【习题3.15】如图3.35所示,齿轮Ⅰ在齿轮Ⅱ内滚动,其半径分别为r和R=2r,曲柄OO1绕O轴以等角速度ωO转动,并带动行星齿轮Ⅰ,求该瞬时轮Ⅰ上瞬时速度中心C的加速度。

图3.35 习题3.15图

图3.36
【解】作平面运动的行星齿轮Ⅰ在图中所示位置的速度瞬心在其与定齿轮Ⅱ的啮合点C上,故vC=0。


图3.37 习题3.16图

图3.38

图3.39
【解】(1)AB杆速度瞬心在O点

(2)以A为基点,有:
![]()
投影在O1B方向:

投影在垂直于O1B的方向:


图3.40 习题3.17图
【解】(1)以A为基点,分析杆AB上点B的速度和加速度,如图3.40(b)、(c)所示。
由于
![]()
由速度分析图得:
![]()
由加速度分析图得:
![]()
将上式分别向B的滑道及垂直于滑道的方向投影,有
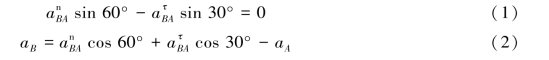
由式(1)、式(2)解得
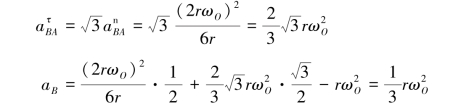
(2)以B为基点,分析杆BC上点C的速度和加速度,如图3.40(b)、(c)所示。由图3.40(b)得

由图3.40(c)得
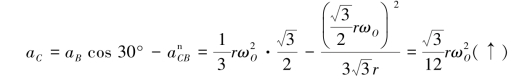
【习题3.18】在如图3.41所示平面机构中,AC杆在导轨中以匀速v平动,通过铰链A带动AB杆沿导套O运动,导套O与杆AC的距离为l。图示瞬时AB杆与AC杆的夹角为φ=60°,求此瞬时AB杆的角速度及角加速度。

图3.41 习题3.18图

图3.42
【解】以O点为坐标原点建立如图3.42所示的直角坐标系,则A点的x坐标为xA=lcotφ
![]()
再将其两端对时间求导,得

![]()
角加速度

【习题3.19】在如图3.43所示的四边形机构中,AB=CD=400mm,BC=AD=200mm,曲柄AB以匀角速度ω=3rad/s绕A点转动,求CD垂直于AD时BC杆的角速度及角加速度。

图3.43 习题3.19图

图3.44
【解】在△ADC中,AC2=AD2+CD2,
在△ABC中,AC2=AB2+CB2-2AB·CBcos∠ABC
AD=BC,AB=CD,这样cos∠ABC=0,有AB⊥BC,由此可知:△ADC≅△ABC
经计算,有

由BC作平面运动得:
![]()
上式在y轴上的投影为:

上式在x轴上的投影为:

【习题3.20】如图3.45所示,轮O在水平面上滚动而不滑动,轮心以匀速vO=0.2m/s运动。轮缘上固连销钉B,此销钉在摇杆O1A的槽内滑动,并带动摇杆绕O1轴转动。已知:轮的半径R=0.5m,在图示位置时,AO1是轮的切线,摇杆与水平面间的交角为60°。求摇杆在该瞬时的角速度和角加速度。

图3.45 习题3.20图
【解】(1)运动分析轮O上点B为动点,动系固结于O1A;绝对运动为平面曲线(摆线),相对运动沿O1A直线,牵连运动为绕O1定轴转动。
(2)速度分析,如图3.45(b)所示。
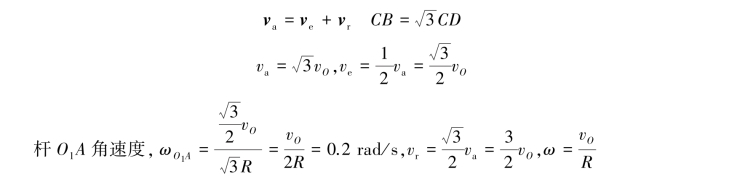
(3)加速度分析,如图3.45(c)所示。
①轮O作平面运动,以O为基点,aO=0,α=0

②轮O上点B为动点,动系固结于O1A:
![]()
上式向aB方向投影,得

杆O1A角加速度


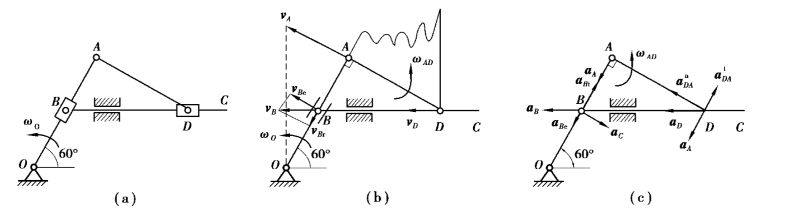
图3.46 习题3.21图
【解】(1)运动分析。BC上B为动点,动系固结于OA;绝对运动为水平直线,相对运动沿直线OA,牵连运动为绕O定轴转动。
(2)速度分析。

AD作平面运动,用速度投影定理,得

套筒D相对杆BC速度为
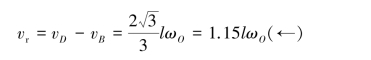
找AD的瞬心P,得

(3)加速度分析。

将上式向aC方向投影,得
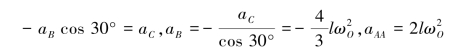
以A为基点:
![]()

套筒D相对杆BC的加速度

【习题3.22】如图3.47所示平面机构中,轮沿地面作纯滚动,通过铰接的三角形板与套筒A铰接,并带动直角杆EGH作水平移动。已知:轮半径为r,O1B=r,三角形各边长为2r,轮心速度为vO。在图示位置时O1B杆水平,B,D,O三点在同一铅垂线上。求该瞬时EGH杆的速度。
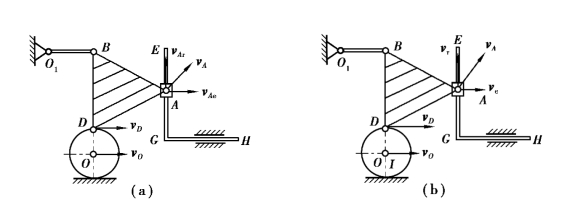
图3.47 习题3.22图
【解】运动机构分析表明,三角形ABD及轮O均作平面运动,由vB的方向,vD的方向确定出三角形ABD的速度瞬心B,轮O的速度瞬心I,各点速度如图3.47(b)所示,有

以A为动点,动系固结在直角杆EGH上,动点A的速度图如图3.47(b)所示,由速度合成定理:va=vr+ve沿水平方向投影,有
![]()
所以vAa=2rωABD=2vO,ve=vO,即直角杆EGH的速度。
【习题3.23】如图3.48所示平面系统,三角形物块以速度v、加速度a向右平移,倾角为θ。BD杆置于铅垂滑道内与AB杆铰接,AB杆长l,位置水平。求图示瞬时AB杆的角加速度。

图3.48 习题3.23图

图3.49
【解】动点为D,动系为三角形物块,牵连运动为平动。
![]()
研究AB杆,以B为基点,有
![]()
【习题3.24】如图3.50所示系统,与OA杆铰接的套筒A带动BD杆沿水平滑道移动,BD杆与做纯滚动的轮铰接。OA杆与轮半径r等长,倾角为φ,其角速度ω0为常量。求轮瞬心C点的加速度。

图3.50 习题3.24图

图3.51
【解】轮D做纯滚动,则
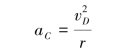

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




