【习题1.1】设动点从x轴上O点,按x=v0t-2t2的规律运动,求动点速度为零的位置,动点回到O点时其速度的大小。

【习题1.2】一点按x=t3-12t+2的规律沿直线运动(其中t以s计,x以m计)。试求:(1)最初3s内的位移;(2)改变运动方向的时刻和所在位置;(3)最初3s内经过的路程;(4)t=3s时的速度和加速度;(5)点在哪段时间作加速运动,哪段时间作减速运动?
【解】(1)将t=3s代入x=t3-12t+2=7m(求得最初3s内位移)
![]()
当速度为零时,有:3t2-12=0,t=2s(即经过2s后速度为零)
x=23-12×2+2=-14m,此时位置坐标x=-14m
(3)在开始的2s内:
t=0时,x=2m
t=2s时,x=-14,路程为16m
t=3s时,x=-7,即2s至3s的路程为7m,总路程为23m
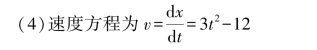
当t=3s时,v=3×32-12=15m/s
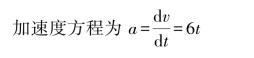
当t=3s时,加速度为18m/s2
(5)因为加速度a=6t>0,始终为x轴的正向。速度前2s时与加速度方向相反,速度从-12到0,为减速运动;2s以后,速度与加速度方向相同,为加速运动。
【习题1.3】分析下列论述是否正确:
(1)点作曲线运动时,加速度的大小等于速度的大小对时间的导数。
(2)点作直线运动时,法向加速度等于零。因此,若已知某瞬时点的法向加速度等于零,则该点作直线运动。
(3)点作曲线运动时,即使加速度的方向始终与速度方向垂直,点也不一定作匀速圆周运动。
【解】(1)错误。曲线运动时加速度有法向加速度和切向加速度两个分量,切向加速度的大小才是速度大小对时间的导数。
(2)错误。法向加速度在切向速度为零时也为零。
(3)正确。运动轨迹不一定是圆周。
【习题1.4】设点作曲线运动,试问如图1.3所示的各种速度与加速度情形,哪些是可能的,哪些是不可能的?为什么?
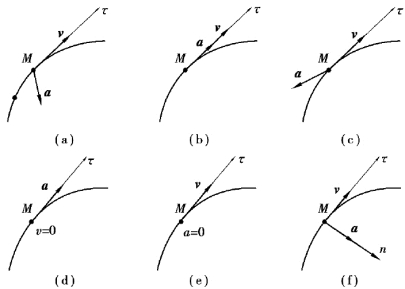
图1.3 习题1.4图
【解】(a)可能,速度方向与切向加速度方向相反,减速运动;
(b)不可能,法向加速度为零的条件是速度为0,或者作直线运动;
(c)不可能,法向加速度的方向要指向曲率中心;
(d)可能,速度为0的情况下法向加速度也为0,点只有切向加速度;
(e)可能,加速度为0,点保持匀速直线运动;
(f)可能,只有法向加速度,作匀速曲线运动。
【习题1.5】已知动点的运动方程为y=bt,φ=ct,b和c均为常数,如图1.4所示。试分别用直角坐标和极坐标写出点的轨迹方程。
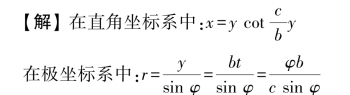
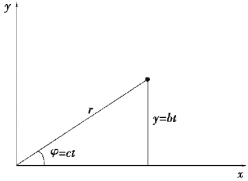
图1.4 习题1.5图
【习题1.6】如图1.5所示,杆AB长l,以等角速度ω绕点B转动,其转动方程为φ=ωt。而与杆连接的滑块B按规律s=α+bsinωt沿水平一作谐振动。其中a和b均为常数。求点A的轨迹。
【解】应用直角坐标法,点A的运动方程为
![]()
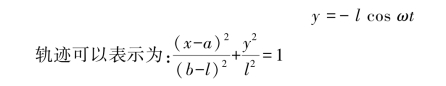

图1.5 习题1.6图

图1.6 习题1.7图
【习题1.7】如图1.6所示,从水面上方高h=20m的岸上一点A,用长40m的绳系住小船。设以等速u=3m/s拉绳。使船靠岸。问在5s末船的速度多大?在5s内船走了多少路程?5s以后,岸上的绳头向左移动了:
![]()
![]()
5s后河面上的绳索缩短为:
![]()
此时小船距离岸边:
![]()
5s小船移动的距离是:
![]()
小船的运动方程为:x2=(40-ut)2-h2;
方程两边对时间求导,得:2xx·=-2u(40-ut);
当t=5s时,x=15,此时小船的速度为:
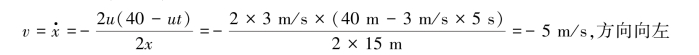

图1.7 习题1.8图
【习题1.8】一根杆子穿过可绕定点B转动的套管,杆的A端以匀速c沿固定水平直线Ox滑动。求杆上M点的运动方程和轨迹方程。设AM=OB=h。
【解】(1)求M点的运动方程:
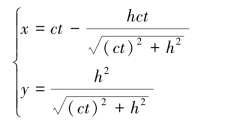
(2)求M点的轨迹方程:
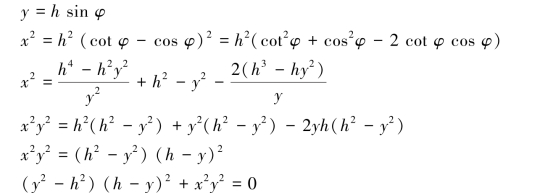
【习题1.9】曲柄OB的转动规律为φ=2t,它带动杆AD,使杆AD上的A点沿水平轴Ox运动,C点沿铅直轴
Oy运动,如AB=OB=BC=CD=12cm,求D点的轨迹方程,求并当φ=45°时杆上D点的速度。
【解】D点的运动方程:
![]()
联立上述两式,消去t可得D点的轨迹方程如下:


图1.8 习题1.9图
D点的速度:
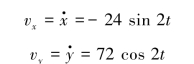
![]()
【习题1.10】刨床急回机构如图所示。r,h,H均为已知,曲柄OA的转动规律为φ=ωt(ω为常数)。求滑块C沿水平轨道滑动的速度和加速度。

图1.9 习题1.10图
【解】以O1点为原点建立直角坐标系,滑块C的位置有x确定,根据三角比关系有:
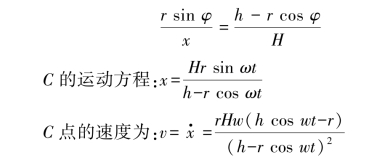
C点的加速度为:
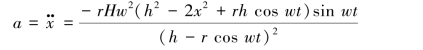
【习题1.11】若三级火箭在A点脱离时,其速度为u=15000km/h,脱离时速度与水平线夹角为45°,然后在没有推力作用的情况下飞行到B点,到B点后发动机才打开。这时轨道与水平一的夹角为20°。在从A点到B点这段时间间隔内,引力加速度的大小和方向均可认为不变,可取g=9m/s2。求从A点到B点所需的时间t(这个时间对设计点火控制系统时有用),并求在这过程中高度的增量h。
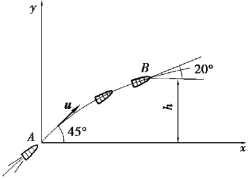
图1.10 习题1.11图
【解】在任一瞬时第三级火箭的加速度在x,y方向上的投影为:
![]()
积分一次后,可得:
![]()
选第三级火箭刚脱离时的点A为初瞬时点,则有t=0时:
![]()
把这个初始条件代入上式,可得:
![]()
设第三级火箭飞行到B点时速度为v,则有:
![]()
因此可得:
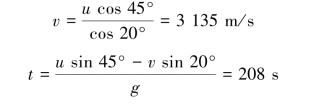
上升高度:
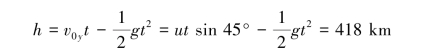
【习题1.12】杆AB在半径等于r的固定圆环半面中以匀速度u沿垂直于杆本身的方向移动。求同时套在杆与圆环上的小环M的自然形式的运动方程及其速度。设初瞬时,小环M在大环的最高点M。以后向右运动。
【解】由自然法有:s=M0M=rφ
![]() (https://www.xing528.com)
(https://www.xing528.com)
所以小环的自然运动方程为:
![]()
其速度为:
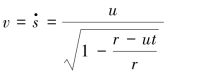
【习题1.13】一点M由静止开始作匀速圆周运动。试证明该点的全加速度和切向速度的夹角α与经过的那段圆弧对应的圆心角β之间存在如下关系:tanα=2β。v=at。
![]()
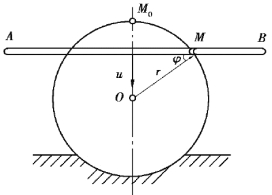
图1.11 习题1.12图
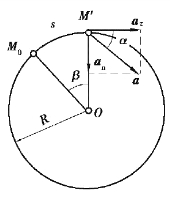
图1.12 习题1.13图
动点A的法向加速度可表示为:

动点A的全加速度与切线间的夹角α可表示为:
证毕。

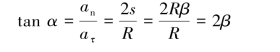
图1.13 习题1.14图
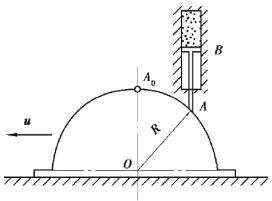
图1.14 习题1.15图

直角坐标方程:

【习题1.15】如图1.14所示,半圆形凸轮以等速u=1cm/s沿水平方向右运动,而使活塞杆AB沿铅直方向运动。当运动开始时,活塞杆A端在凸轮的最高点上。如凸轮的半径R=8cm,求活塞B相对于地面和相对于凸轮的运动方程和速度。
【解】(1)A相对于地面运动,直角坐标系固连在地面上。则A的运动方程为:
![]()
A的速度为:
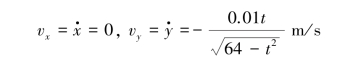
A相对于凸轮的运动为圆周运动,其自然方程为:
![]()
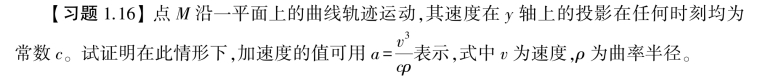
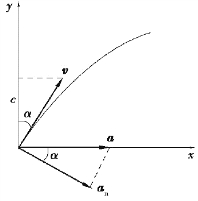
图1.15 习题1.16图
![]()
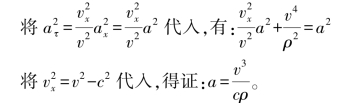
【证明】方法(1):设全加速度为a,法向加速度为an,依题意有矢量关系图:
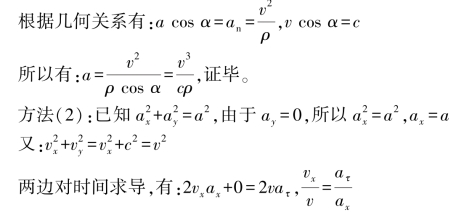
【习题1.17】炮弹的发射角为α,初速度为v0,空气阻力略去不计。试求炮弹在其速度与水平线成θ角处的法向加速度、切向加速度以及轨迹在该点的曲率半径。
【解】由题意有矢量关系图,根据几何关系有:
![]()
又因a=g,所以有:
![]()
因为vx=v0cosα=vcosθ
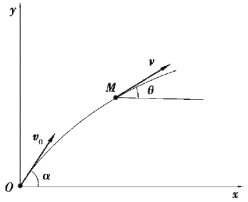
图1.16 习题1.17图

【习题1.18】已知某动点用极坐标表示的运动方程为:ρ=3+4t2,φ=1.5t2。求φ=60°时点的速度与加速度。ρ的单位为m,φ的单位为rad,t的单位为s。
【解】
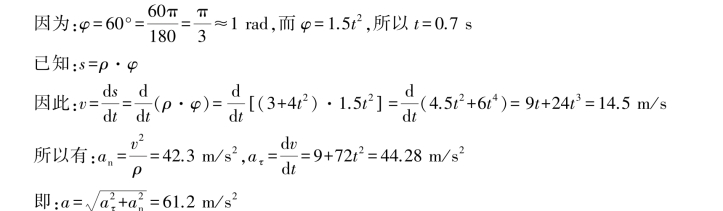
【习题1.19】如图1.17所示的曲柄滑杆机构中,滑杆有一圆弧形滑道,其半径R=100mm,圆心O1在导杆BC上。曲柄长OA=100mm,以等角速度ω=4rad/s绕轴O转动。求导杆BC的运动规律,以及当曲柄与水平线间的交角为30°时,导杆BC速度和加速度。
【解】t瞬时:
滑块的x坐标:

图1.17 习题1.19图
![]()
O1的坐标x
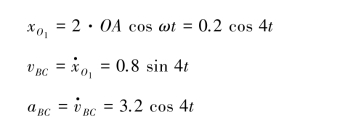

图1.18 习题1.20图
φ=30°时
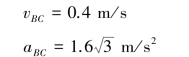
【习题1.20】如图1.18所示,曲柄CB以等角速度ω0绕轴C转动,其转动方程为φ=ω0t。滑块B带动摇杆OA绕轴O转动。设OC=h,CB=r,求摇杆的转动方程。
【解】由于rsinφ=(h-rcosφ)tanθ
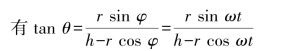
其OA杆的转动方程为:
![]()
【习题1.21】如图1.19所示,纸盘由厚度为a的纸条卷成,令纸盘的中心不动,而以等速v拉纸条。求纸盘的角加速度(以半径r的函数表示)。
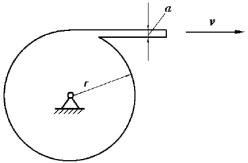
图1.19 习题1.21图
【解】纸盘作定轴转动,当纸盘转过2πrad时半径减小a,设纸盘转过dθ时半径增加dr,则纸盘的角速度为:

又rω=v,两边对时间t求导:
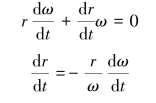
即得纸盘的角速度:
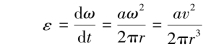


图1.20 习题1.22图

图1.21 习题1.23图
【解】AB平移,所以轮B上与轮2接触点D处:
![]()
因为齿1,轮2啮合,所以轮2上点D速度与轮1上点D速度相同,切向加速度也相同:

【习题1.23】如图1.21所示,飞轮绕固定轴O转动,在运动过程中,其轮缘上任意一点的全加速度与轮半径的交角恒为60°。当运动开始时,其转角φ0等于零,其角速度为ω0,求飞轮的转动方程,以及角速度和转角间的关系。
【解】设轮缘上1点M的全加速度为a,切向加速度at=rα,法向加速度an=ω2r
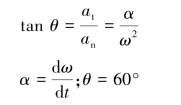
联立上面两式得:
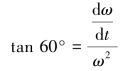
分离变量后,两边积分得:
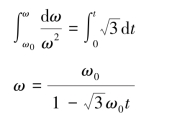
又因为:
![]()
所以有:
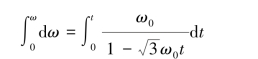
得飞轮的转动方程为:
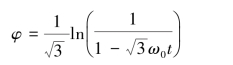
即:

飞轮角速度与转角的关系为:
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




