利用线性回归转化非线性回归模型的方法

前几节都是在两变量之间的内在关系为线性关系时讨论回归分析问题,但是,在实际中有时两变量之间的内在关系是非线性关系,即E(Y|X=x)=f(x;β0,β1)是非线性的。例如,在细菌培养实验中,每一时刻的细菌总量观测值y 与时间x 的趋势关系是指数关系,即y=另一种情形,是在根据理论和经验无法推知x 和y 之间的函数类型时,只能根据试验数据选取恰当类型的函数曲线来拟合。在拟合曲线时,在参照散点图的基础上,最好用不同函数类型计算后进行比较,选取某个优良性准则下最好的一种曲线拟合方法。

一个方向是希望所选择的拟合曲线与观测数据(xi,yi)(i=1,2,…,n)拟合较好。通常用残差平方和

或相关指数

的值来衡量拟合曲线的好坏程度,其中越小或R2 越大,表明拟合效果越好。有关非线性回归模型已有丰富的研究,由于本书内容特征所限,不再赘述。

本节主要考虑针对所选取的曲线函数,可以通过适当的变换,将变量间的关系式化为线性形式,如下所示。

①对于双曲线,则y′=β0+β1x′+ε,ε～N(0,σ2)。

②对于幂函数曲线y=dxβ1ε,lnε～N(0,σ2),若令y′=lny,x′=lnx,β0=lnd,ε′=lnε,则y′=β0+β1x′+ε′,ε′～N(0,σ2)。

③对于对数函数曲线y=β0+β1lnx+ε,ε～N(0,σ2),若令x′=lnx,则y=β0+β1x′+ε,ε～N(0,σ2)。

④对于指数函数曲线y=deβ1xε,lnε～N(0,σ2),若令y′=lny,β0=lnd,ε′=lnε,则y′=β0+β1x+ε′,ε′～N(0,σ2)。

⑤对于S 型曲线,如图10.5.1 所示,若令e-x,则y′=β0+β1x′+ε,ε～N(0,σ2)。

图10.5.1

例10.5.1 为了考察某市百货商店的销售额x 与流通费用率y 之间的关系,表10.5.1列出了该市9个商店的销售额与流通费用率的统计数据,求y 关于x 的回归方程。(www.xing528.com)

表10.5.1

解 作散点图,从图10.5.2中可以看出y 随x 的增加而减少,它们之间大致呈双曲函数关系或幂函数关系。

图10.5.2

先考察双曲函数关系,即,则有y′=β0+β1x′,这是线性回归方程,从而可用最小二乘法估计β0 和β1,经计算得Sx′y′=-0.165938,从而

于是得回归方程

经检验,在显著性水平α=0.05下,回归方程(10.5.3)的线性关系显著,根据回归方程计算对应于各xi 的回归值,以及残差平方和具体计算结果如表10.5.2所示。

表10.5.2

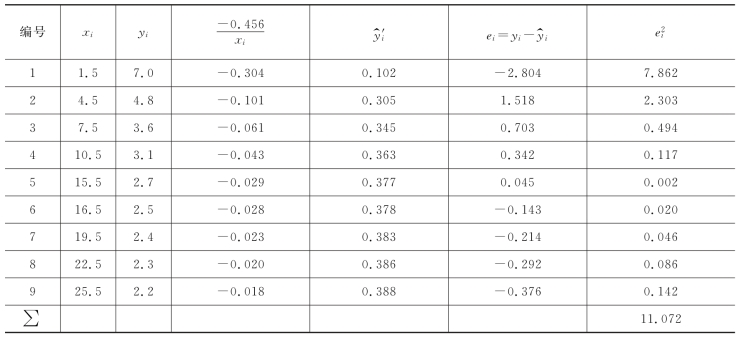
从表10.5.2中可以看出,残差平方和S2e≈11.072,总平方和Syy=22.5,相关指数R2==0.492,销售额与流通费用率的简单相关系数的平方和ρ2=0.7534,因此,两者是不同的。

再考察x 与y 之间的幂函数关系y=β0xβ1,得回归方程y=8.520972x-0.423293,残差平方和S2e=0.0070212,相关指数R2=0.99421。因此,拟合幂函数曲线比拟合双曲线的实际效果要好。另外,在对y 进行预测时,可先对y′进行预测,再将y′的预测区间变换到y 的区间。