F检验结果表明回归方程的线性效果显著

考虑y 的n 个观测值y1,y2,…,yn 的总离差平方和分解:

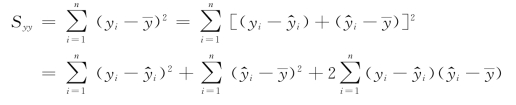
因为交叉项

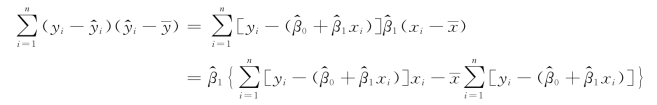
由正规方程(10.2.3)得交叉项为零,于是

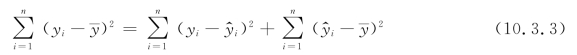
此平方和分解如图10.3.1所示。

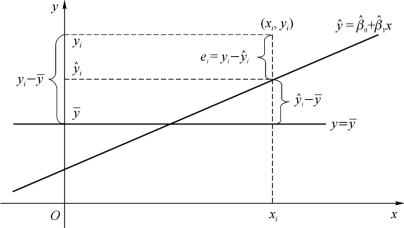
图10.3.1

令

则

其中S2R 称为回归平方和,S2e 称为残差平方和。若β1=0,则回归直线 就变成和直线重合,此时S2R 应为零。因此,S2R 表示由X 的变化引起的Y 的变化,它反映了Y的变差中Y 随X 作线性变化的部分。S2R 在Syy中的比例越大,表明X 对Y 的线性影响越大,即Y 对X 的线性关系越显著。另一方面,若Y 完全由X 确定,则给定X=xi 时,Y 的观测值yi 应等于其回归值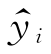,S2e 应为零,因此S2e 是除X 对Y 的线性影响外的一切随机因素所引起的Y 的变差部分。S2e 在Syy中的比例越大,S2R 在Syy中的比例越小,这表明由X 的变化而引起的Y 的线性变化部分淹没在由随机因素引起的Y 的变化中,这时Y 对X 的线性关系不显著,回归方程也就失去了实际意义。因此,可利用比值(www.xing528.com)

作为检验假设(10.3.2)的检验统计量。当F 值较大时,拒绝原假设H0;当F 值较小时,不能拒绝H0。可以证明:①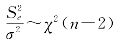)且S2e 与S2R 相互独立;②当H0 成立时,于是,当H0 成立时,F=

给定显著性水平α,当F＞Fα(1,n-2)时拒绝H0,即认为Y 对X 的线性关系显著;反之,认为Y 对X 的线性关系不显著。以上检验过程可归纳成表10.3.1所示的方差分析表。

表10.3.1

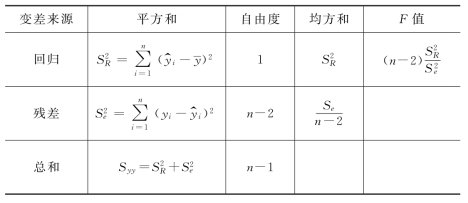
Syy,S2R,S2e通常按下列各式计算:

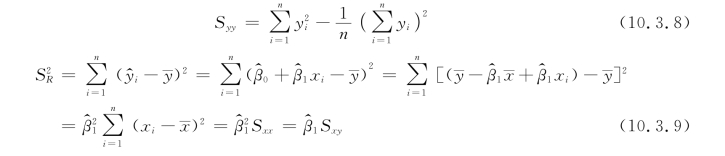
例10.3.1 给定显著性水平α=0.05,试检验例10.1.1中的回归方程(10.2.8)的线性效果是否显著。

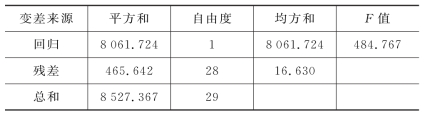
解 由式(10.3.8)～式(10.3.10),经Excel计算得表10.3.2所示的方差分析表(表10.2.1的部分输出结果)。

查表得F0.05(1,28)=4.20＜484.767,因此拒绝H0,认为当显著性水平α=0.05时,回归方程(10.2.8)的线性效果显著。

表10.3.2