最小二乘估计方法实践

利用n对观测数据(xi,yi)(i=1,2,…,n),在式(10.1.2)和式(10.1.3)的假定下,估计模型中的参数β0,β1。将式(10.1.2)重新表达成

于是,ε1,ε2,…,εn 反映了数据点(xi,yi)对回归直线竖直方向的偏离程度,我们当然希望这些偏离越小越好,衡量这些偏离大小的一个合理的指标是它们的平方和。令

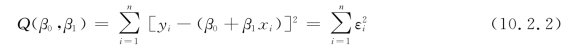
参数β0,β1 的估计值满足

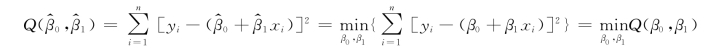
为此,分别取Q 关于β0,β1 的偏导数,并令它们等于0:

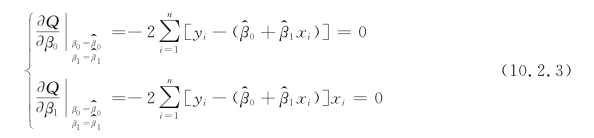
方程组(10.2.3)称为正规方程。

上述方程组的解记为它们的表达式如下:

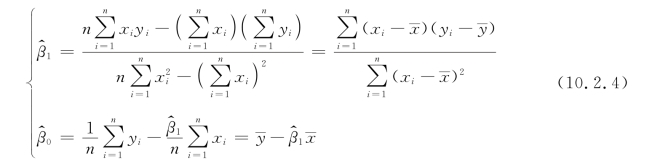
其中,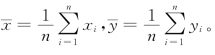上述估计使误差平方和达到最小,这种估计方法称为最小二乘法(leastsquaresmethod),式(10.2.4)确定的 称为β0,β1 的最小二乘估计(Least SquaresEstimates,LSE)。

若 分别是β0,β1 的最小二乘估计,则对于某个给定的x,取 作为y 的预测。方程 称为y 关于x 的最小二乘线性回归方程,其图形为回归直线分别为直线的截距和斜率 使得所有数据点(xi,yi)(i=1,2,…,n)在竖直方向上离回归直线的距离平方和最小。记

称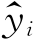为x=xi 时y 的回归值,称ei 为残差,即观测值与回归值之差。

我们注意到,将其代入线性回归方程 得(www.xing528.com)

式(10.2.5)表明回归直线经过散点图的几何中心

为了计算方便,记

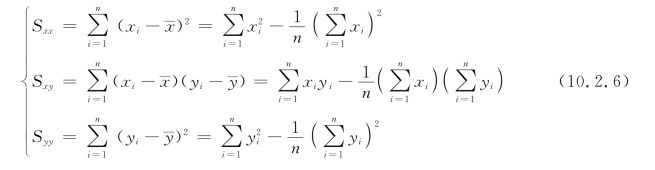
则

例10.2.1 根据表10.1.1给出的观测数据,确定y 对x 的线性回归方程。

解 根据式(10.2.6)得Sxx=7380.7,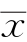=45.9,Sxy=-7713.7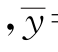=148.7667,进而得

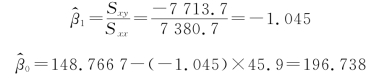
于是,线性回归方程为

现代统计学已经和计算机科学密不可分了,在理解上述最小二乘估计思想的基础上,使用许多常见的计算软件,如Excel、R、SPSS、SAS、MATLAB 等,可以方便快捷地求出上述估计值。下面以Excel软件为例,简要介绍求解最小二乘估计的步骤,详细步骤可参考Excel工具书。

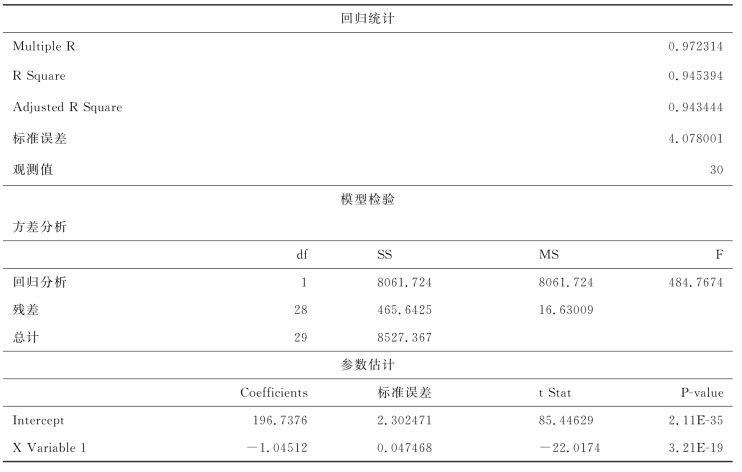
将表10.1.1给出的观测数据录入Excel。然后,单击Excel中的“工具”菜单,可见数据分析选项。用鼠标双击“数据分析”选项,弹出“数据分析”对话框,然后选择“回归”,确定后,最后选择X,Y 值合适的输入区域,选择一定的参数设置后,易得表10.2.1所示的结果。表10.2.1中的“Coefficients”一列的两个值依次为模型中截距项(Intercept)的估计β^0 和回归系数的估计β^1 的值。

表10.2.1