双因素无重复试验方差分析结果

通过前面的讨论,若交互作用存在,则对于每一试验条件(Ai,Bj),必须做重复试验,只有这样才能将交互效应平方和从总的离差平方和中分解出来。在实际中,如果我们已经知道不存在交互作用,或已知交互作用对试验结果的影响很小,则可以不考虑交互作用,这时不必做重复试验,对于两个因素的每一组合(Ai,Bj)只做一次试验,所得结果如表9.2.8所示。

表9.2.8

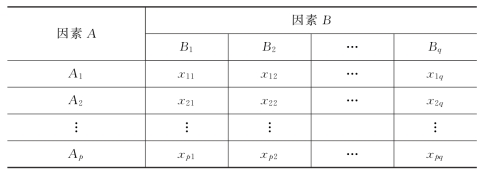
双因素无重复试验的方差分析数据由于不存在交互作用,无重复试验,因此r=1,γij=0(i=1,2,…,p;j=1,2,…,q),于是模型可写成:

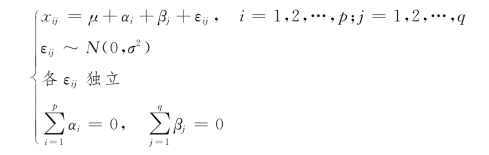
根据上述模型,我们要检验以下两个假设:

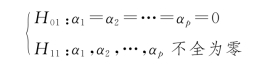
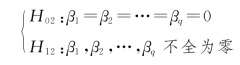
相应的方差分析表如表9.2.9所示。

表9.2.9

表9.2.9中,

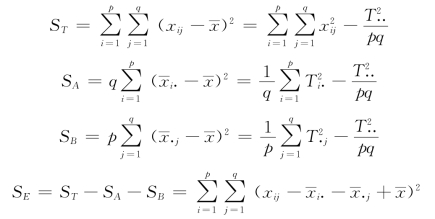
其中,

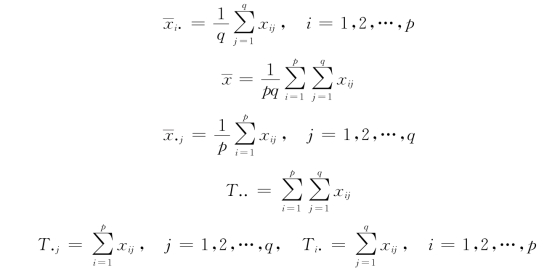
取显著性水平α,当FA ＞Fα(p-1,(p-1)(q-1))时,拒绝H01;当FB ＞Fα(p-1,(p-1)(q-1))时,拒绝H02。

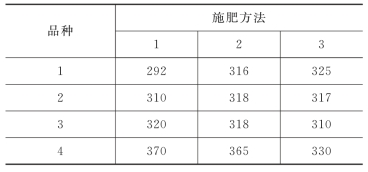
例9.2.5 在一个小麦农业试验中,考虑4种不同的品种和3种不同的施肥方法,小麦亩产量数据(单位:kg)如表9.2.10所示。试在水平α=0.05下,检验小麦品种和施肥方法对小麦亩产量是否存在显著影响。

表9.2.10(www.xing528.com)

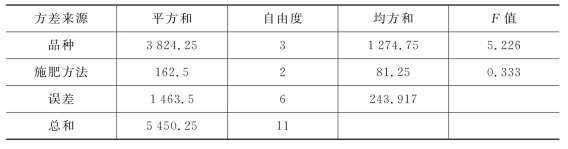
利用公式计算得方差分析表,如表9.2.11所示。查表得F0.05(2,6)=5.14,F0.05(3,6)=4.76,从而在α=0.05下,施肥方法对小麦亩产量无显著影响,但小麦品种对产量有显著影响。

表9.2.11

例9.2.6 在某种橡胶的配方中,考虑了3种不同的促进剂(A),4种不同分量的氧化锌(B),各种配方试验一次,测得300%定强如表9.2.12所示,试检验不同促进剂、不同分量的氧化锌分别对定强有无显著影响。

表9.2.12

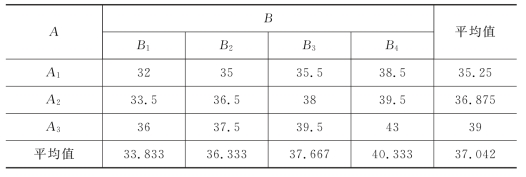
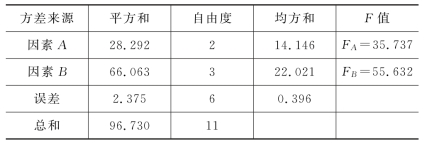
解 由题可知p=3,q=4,n=pq=12,得方差分析表,如表9.2.13所示。给定α=0.05,查得F0.05(2,6)=5.14,F0.05(3,6)=4.76,易见FA ＞F0.05(2,6),FB ＞F0.05(3,6),所以拒绝H01,H02,即不同促进剂和不同分量的氧化锌对橡胶定强均有显著影响。

表9.2.13

从前面的分析可以看出,对于双因素试验,在每个试验条件下做重复试验,其试验次数已经很多,且方差分析的计算量明显过大,那么对于三因素或更多因素的试验,若做全面试验(即每个试验条件下均做试验),则相应的试验次数和计算量会呈指数形式增长。

例如,一个试验中涉及4个因素A,B,C,D,分别有p,q,r,s个水平,每个试验条件下重复做t次试验,则共需要做pqrst次试验,这样试验次数往往太多,实施起来不太现实。因此,在实际应用中,一般只做部分实施,即在pqrs个试验条件中选出一部分试验条件,然后在这一部分试验条件下做试验。当然,这一部分条件不是任意选取的,它们必须满足以下3个条件:

①具有一定的代表性;

②根据这些试验数据能够估计出模型中的所有参数;

③总的离差平方和能够进行相应的分解。

至于如何选取试验条件,这是试验设计(如正交设计、均匀设计等)的内容,其细节已远超出本课程的范围,本书不作讨论。