《概率论与数理统计》中的重要成果

例9.2.2 某工序给零件镀银,测试了3种不同配方在2种工艺下镀上银层的厚度,在每个试验条件下进行了2次试验,数据(单位:μm)如表9.2.2所示。

这里有两个因素,一个因素是配方,另一个因素是工艺,它们同时影响着银层厚度。由于存在两个因素,因此,除了要分别考察每个因素对银层厚度的影响外,还要研究不同配方和不同工艺对银层厚度的联合影响是否恰好是每个因素分别对银层厚度的影响的叠加。例如,当不考虑随机因素的干扰时,如果将配方固定为A1,采用工艺乙时比采用工艺甲时银层的厚度薄1μm,如果将工艺固定为工艺甲,采用配方A3 时比采用配方A1 时银层的厚度薄3μm,而采用配方A3、工艺乙时银层的厚度并非比采用配方A1、工艺甲时银层的厚度薄1+3=4μm。也就是说,是否产生这样的情况,即分别使银层厚度达到最薄的配方与工艺搭配在一起可能会使银层厚度大大增加,而看起来不是最优的配方和工艺搭配在一起,由于搭配得当而使银层厚度大大变薄。这种由各个因素的不同水平的搭配所产生的新的影响称为交互作用,这是多因素试验方差分析不同于单因素试验方差分析之处。

表9.2.2

一般地,设影响试验结果的两个因素为A 和B,因素A 有p 个水平A1,A2,…,Ap,因素B有q个水平B1,B2,…,Bq,在每一试验条件(Ai,Bj)下均进行了r次重复试验,得到表9.2.3所示的结果,表中每组数据{xij1,xij2,…,xijr}可认为是来自同一总体的样本,假定

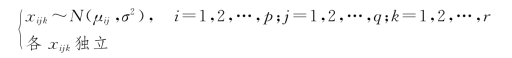
xijk可写成xijk=μij+εijk,其中εijk～N(0,σ2)且各εijk相互独立,令

称μ 为总平均,称αi 为水平Ai 的效应,称βj 为水平Bj 的效应,称γij为水平Ai 和Bj 的交互效应。易见

于是双因素试验的方差分析模型可写为

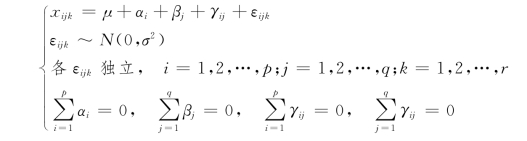
表9.2.3

对上述模型,要分别检验因素A、因素B、因素A 与B 的交互作用对试验结果是否有显著影响,即检验以下3个假设:

为此需分别建立检验统计量,记

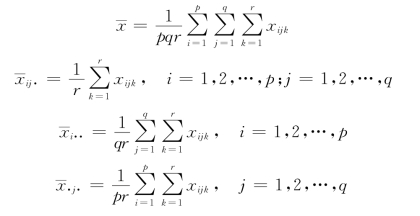
则总的离差平方和

其中,

称SE,SA,SB,SA×B分别为误差平方和、因素A 的效应平方和、因素B 的效应平方和、A 与B的交互效应平方和。

在模型的假定下,可以证明如下结论:

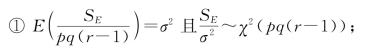
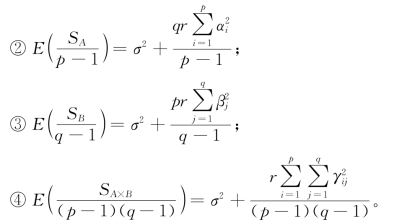(www.xing528.com)

构造检验统计量:

其中pq(r-1),p-1,q-1,(p-1)(q-1)分别是SE,SA,SB,SA×B的自由度。

可以证明:当假设H01成立时,且与SE 独立,所以FA～F(p-1,pq(r-1))。当假设H02成立时,～χ2(q-1),且与SE 独立,所以FB～F(q-1,pq(r-1))。当假设H03成立时～χ2((p-1)(q-1)),且与SE独立,所以FA×B～F((p-1)(q-1),pq(r-1))。

取显著性水平α,当FA＞Fα(p-1,pq(r-1))时,拒绝H01;当FB＞Fα(q-1,pq(r-1))时,拒绝H02;当FA×B＞Fα((p-1)(q-1),pq(r-1))时,拒绝H03。

上述结果可汇总成表9.2.4所示的方差分析表。

表9.2.4

实际计算中,可按下列各式计算各个平方和:

其中

例9.2.3 在例9.2.2中,假定双因素方差分析所需的条件均满足,试在水平α=0.05下,检验不同配方(因素A)、不同工艺(因素B)下的银层厚度是否有显著差异,配方和工艺的交互作用是否显著,配方和工艺分别取何水平时,银层厚度最薄。

解 根据表9.2.2中的数据,利用上述公式计算得方差分析表,如表9.2.5所示。查F分位数表得F0.05(2,6)=5.14,F0.05(1,6)=5.99。由此可见,在水平α=0.05下,不同配方下的银层厚度无显著差异,而不同工艺下的银层厚度有显著差异,且配方和工艺的交互作用显著,由表9.2.2中的数据可知,采用配方A3 和工艺甲时银层厚度最薄。

表9.2.5

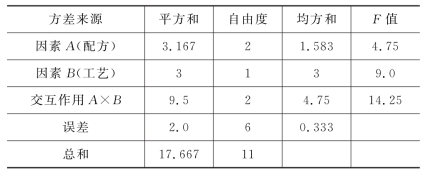
例9.2.4 考虑合成纤维中对纤维弹性有影响的2个因素:收缩率A 和总拉伸倍数B。A和B 各取4种水平,整个试验进行2次,试验结果如表9.2.6所示。试检验收缩率和总拉伸倍数分别对纤维弹性有无显著影响,并检验二者对纤维弹性有无显著性交互作用(给定显著性水平α=0.05)。

表9.2.6

解 按题意p=q=4,r=2,n=32,计算得表9.2.7所示的双因素方差分析表。

表9.2.7

对于α=0.05,查表得F0.05(3,16)=3.24,F0.05(9,16)=2.54。比较可知FA＞3.24,FB＜3.24,FA×B＞2.54,所以拒绝H01和H03,而接受H02,即合成纤维的收缩率对弹性有显著影响,总拉伸倍数对弹性无显著影响,而二者对弹性有显著的交互作用。