双因素试验方差分析结果

在实际问题中,一般遇到的影响指标的因素都不止一个,如例9.1.3中影响产出率的因素,除反应时间外,还有反应温度、搅拌速度等,这样就要考察哪些因素影响显著,双因素方差分析就是讨论2个因素对试验结果的影响是否显著的有效方法。在双因素试验中,有时会出现这样一种情况:不仅单个因素对试验结果有影响,因素之间的组合作用也会对试验结果产生影响,前者为无交互作用,后者就是交互作用。例如,在小麦生产中,研究几种不同的种子与几种不同的肥料对产量的影响,是否将产量最高的种子与使产量达到最高的肥料搭配到一起,小麦的产量一定会更高呢? 实践证明是不一定的,有时反而是不太好的种子与某种肥料搭配到一起会使产量达到最高,这就是所谓的交互作用影响的结果。

为了更清楚地了解交互作用,下面举一个实际例子。

例9.2.1 在土地情况大致相同的4块大豆试验田上进行试验,考虑氮肥(N)和磷肥(P)对平均亩产量的作用,对磷肥分不施与施4斤两种情形,对氮肥分不施与施6斤两种情形,并且4块田上分别采用不施肥、单独施磷肥、单独施氮肥、同时施磷肥和氮肥4种方法进行试验,所得平均亩产量(单位:斤)如表9.2.1所示。

表9.2.1(www.xing528.com)

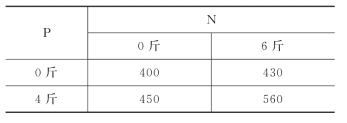
表9.2.1表明,单独施磷肥平均亩产增加50斤,单独施氮肥平均亩产增加30斤,而同时施两种肥料平均亩产增加160斤,因此,两种肥料组合起来的作用是增加亩产160-50-30=80斤,这就是两种肥料的交互作用,它恰好等于表9.2.1主对角线之和(400+560)减去次对角线之和(430+450)。

因素之间是否存在交互作用就是多因素方差分析问题。