方差分析基本思想及应用概率论与数理统计

在一项实验中,如果只有一个因素在改变,其他因素保持不变,则称这种试验为单因素试验,所采用的方法称为单因素方差分析。

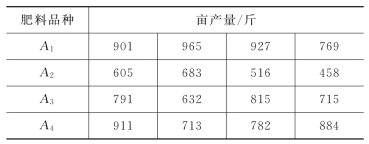
例9.1.1 为了比较4种不同肥料对小麦亩产量的影响,取一片土质等条件相差不多的土地,分成16块。肥料品种记为A1,A2,A3,A4,每种肥料施在4块土地上,得到亩产量如表9.1.1所示(1斤=500g),试问施肥品种对小麦亩产量有无显著影响?

表9.1.1

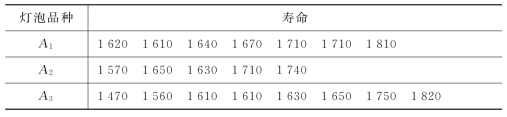
例9.1.2 某灯泡厂用3种不同材料制成的灯丝生产3批灯泡,在每一批中取若干个进行寿命试验,得到表9.1.2所示的数据(单位:小时),试问灯丝的材料对灯泡寿命有无显著影响?

例9.1.1中的肥料和例9.1.2中的灯丝的材料称为因素,其中都只有一个因素。各种肥料和灯丝的材料称为水平,例9.1.1 称为单因素四水平试验,例9.1.2 称为单因素三水平试验。

表9.1.2

在例9.1.1中,施每一种肥料所得小麦的亩产量构成一个总体,共有4个总体。在各总体中分别取一容量为4的样本(即都做4次试验,称为等重复试验),要检验不同肥料所得平均亩产量是否有显著不同,即检验4个总体的均值是否相等。如果各总体均值差别不大,则说明施肥品种对亩产量没有显著影响;如果各不同肥料对应的均值差别较大,则说明施肥品种对亩产量有显著影响。在例9.1.2中,每一种灯丝材料生产出的灯泡的寿命构成一个总体,共有3个总体。从各总体中分别取一样本,容量不等(称为不等重复试验),检验灯丝材料的不同对灯泡平均寿命是否有显著影响,即检验3个总体的均值是否相等。如果各材料对应的灯泡的平均寿命差异不大,则认为灯丝的材料对灯泡的平均寿命没有显著影响;如果各材料对应的灯泡的平均寿命差异较大,则认为这种差异是由“灯丝的材料不同”引起的,即材料对灯泡寿命有显著影响。需要注意的是,这里的各总体的均值(平均亩产量和灯泡的平均寿命)是指理论均值,而不是各总体下样本的实测数据的平均值。检验某因素对试验结果是否有显著影响,就归结为该因素在不同水平下各个总体的(理论)均值是否相等的问题。由于其他条件(或因素)总是尽可能一致,因此可认为每个总体的方差是相同的。在理论上,要检验几个总体的均值是否相等总是要求总体是正态分布的。在例9.1.1和例9.1.2中各水平对应了方差相等的正态总体,推断因素(肥料品种或灯丝的材料)对结果(小麦的亩产量或灯泡的寿命)是否有显著影响的问题等价于推断具有相同方差的正态总体的均值是否相同的问题。这就是单因素方差分析的基本思想。

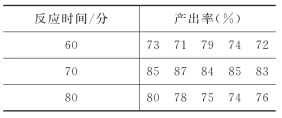
例9.1.3 某化工厂为了探求合适的反应时间以提高其产品(一种试剂)的产出率,在其他条件都加以控制的情况下,对不同的反应时间进行了5次试验,结果如表9.1.3所示。(www.xing528.com)

表9.1.3

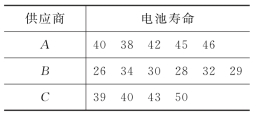
例9.1.4 某企业现有3批电池,它们分别来自3个供应商A,B,C,为评比其质量,各随机抽取几只电池作为样品,经试验得其寿命(单位:小时)如表9.1.4所示。

表9.1.4

以上例子都是单因素试验。从例9.1.3中可以看出,对于不同的反应时间,其产出率存在差异,这种差异可以认为是反应时间这一因素对产出率的影响。在同一反应时间条件下,其产出率也存在差异,这种差异是由其他一些不能控制的次要因素共同作用造成的,可以看作是由随机因素造成的。问题是产出率的差异主要是由反应时间不同造成的,还是由其他随机因素造成的? 即分析反应时间对产出率的影响是否显著,或者说,不同反应时间条件下的产出率是否存在显著差异。

类似地,在例9.1.4中,要考察3个供应商的电池寿命是否存在显著差异。

下面将从上述几个例子中抽象出一般的数学模型。