单边假设检验：单个正态总体|概率论与数理统计

①已知方差σ2,检验H0:μ≤μ0,H1:μ＞μ0。

设(X1,X2,…,Xn)是一个样本,在H0 成立的条件下,易知

于是,对于任何实数λ,都有由检验水平α,查标准正态分布表,得正态分布的临界值uα,使P{U1＞uα}=α,即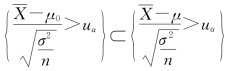都是小概率事件。这时,H0 的否定域可以定为(uα,+∞),由样本观察值计算U0,若U0 落入否定域,即可做出否定H0 的结论。

由此我们得到单侧检验的步骤完全类似于双侧检验,只需要注意它的否定域仅为单侧区间。显然,单侧检验比双侧检验灵敏,这是有代价的,即需要事先对待检验的参数有较多的了解。

例8.2.4 已知某种水果罐头维生素C的含量服从正态分布,标准差为3.98mg。产品质量标准中,维生素C的平均含量必须大于21mg。现从一批这种水果罐头中抽取17罐,测得维生素C的含量的平均值x=23mg。问这批罐头的维生素C含量是否合格(α=0.05)?

解 因为要求维生素C 的平均含量必须大于21mg,少了则判为不合格品,所以用单侧检验。

首先,提出假设H0:μ≤μ0=21,H1:μ＞21。在H0 成立的条件下,

由检验水平α,查标准正态分布表,得临界值uα=1.38,确定否定域为(uα,+∞)。由样本观察值计算得

所以否定H0,即认为这批罐头的维生素C含量符合标准。

类似地,可以得到以下两类单侧检验的否定域。

②未知方差σ2,检验H0:μ≤μ0,H1:μ＞μ0,否定域为(tα(n-1),+∞)。

③未知均值μ,检验H0:σ2≤σ20,H1:σ2＞σ20,否定域为(χ2α(n-1),+∞)。(www.xing528.com)

例8.2.5 用机器包装食盐,假设每袋盐的重量服从正态分布,规定每袋盐的标准重量为500g,标准差不能超过10g。某日开工后,从装好的食盐中随机抽取9袋,测得重量(单位:g)为

这天包装机的工作是否正常(α=0.05)?

解 包装机工作正常是指μ=500和σ2≤102,因此分两步进行检验。

a.由题意,提出假设H0:μ=μ0=500,H1:μ≠500。在H0 成立的条件下,

由给定的检验水平α,查t分布表,得临界值tα/2(8)=2.306,即由样本值计算得

所以不能否定H0,即可以认为平均每袋盐重为500g。

b.提出假设H′0:σ2≤102,H′1:σ2＞102。在H′0成立的条件下,

由给定的检验水平α,查χ2 分布表,得临界值由样本值计算得

所以否定H′0,即可以认为方差超过102,包装机工作不稳定。

综上所述,包装机工作不正常。