统计假设的检验,是指按照一定规则——检验准则,根据样本信息去判断所做假设的真伪,并决定接受还是否定假设。由于假设检验的决定是根据随机样本或统计量做出的,因此任何检验都不能避免错误,选择检验准则的基本原则是要使检验的错误较小。
1.检验准则
判断假设是否成立以决定假设取舍的规则称为检验准则,简称为检验。检验准则常以原假设H0 的否定域形式表示。
否定域也称拒绝域或临界域。假设H0 的否定域V 是给样本值划定的一个范围或在一切样本值的集合(样本空间)中指定的一个区域:当样本值x=(x1,x2,…,xn)属于区域V 时否定H0。应用中,否定域V 常通过选择某个适当的统计量T 来构造,这时,T 称作检验的统计量。以否定域的形式表示的检验只有“否定H0”和“不否定H0”两种可能的决定。
例8.1.1 抽样验收一批产品,若不合格品率p 超过规定的界限p0,则认为这批产品不合格并予以拒收。以νn 表示n 次抽样抽到不合格品的件数。
这是一个“原假设为H0:p≤p0,而对立假设为H1:p>p0”的统计检验问题,可以用V={νn≥c}作为原假设H0 的否定域,其中c是随机抽验的n 件产品中不合格品的临界件数,即当νn≥c时否定H0,并认为这批产品不合格,予以拒收。对于固定的n,确定临界值c的原则是出现错误的概率要小,这时可能出现两种类型的错误:①错误地“拒收合格批”,即这批产品中不合格品率p 本来未超过规定的界限p0,却被错误地拒收了;②错误地“接收不合格批”,即这批产品中不合格品率p 本来超过了规定的界限p0,却被错误地接收了。
2.检验的两类错误
设H0 是关于总体X 的假设,V 是H0 的否定域,(X1,X2,…,Xn)是来自总体X 的简单随机样本。当“随机点”(X1,X2,…,Xn)落入否定域V 时,即当事件RV={(X1,X2,…,XN)∈V}出现时否定H0。由于统计检验的结论是根据随机样本(X1,X2,…,Xn)的取值做出的,而这个随机样本的取值总是既可能落入否定域,又可能落入接受域,因此所做决定有可能是错误的。根据原假设H0 的“真”与“伪”以及所做决定是“否定H0”还是“接受H0”,存在表8.1.1所示的四种可能情形,其中两种是正确决定,另外两种则是错误决定。
①第一类错误:否定了本来真实的假设(弃真),称作第一类错误,常表示为α。
②第二类错误:接受了本来错误的假设(纳伪),称作第二类错误,常表示为β。
表8.1.1

由于检验的规则依赖于样本,而样本具有随机性,因此检验的错误出现与否也是随机的,但是我们可以估计和控制检验错误出现的概率。在假设H0 成立的条件下事件RV 出现(原假设为真但否定原假设)的概率,即检验犯第一类错误的概率可以表示为P(RV|H0);在假设H0本来错误(从而H1 成立)的条件下事件RV ={(X1,X2,…,XN)∉V}出现的概率,即检验犯第二类错误的概率表示为P(RV|H1)。
例如,抽样验收一批产品,如果其不合格品率p 超过规定界限p0,则拒收,否则接收。由于这批产品的不合格品率p 未知,因此产生了区分原假设H0:p≤p0 与对立假设H1:p>p0的检验问题。以例8.1.1中的V={νn≥c}作为假设H0 的否定域,则检验的第一类错误概率α和第二类错误概率β分别如下:(https://www.xing528.com)
![]()
第一类错误概率α 和第二类错误概率β 又分别被称为厂方风险和用户风险。
例8.1.2 假定X 是连续型随机变量,X1 是对X 的(一次)观测值,关于其概率密度f(x)有如下假设:
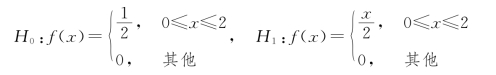
检验规则:当事件![]() 出现时,否定假设H0、接受假设H1。求检验的第一类错误概率α 和检验的第二类错误概率β。
出现时,否定假设H0、接受假设H1。求检验的第一类错误概率α 和检验的第二类错误概率β。
解 由检验的两类错误概率α 和β 的意义,知
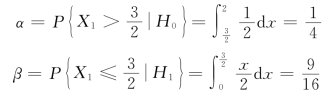
例8.1.3 假定总体X~N(μ,1),关于总体X 的数学期望μ 有两个假设:
![]()
设(X1,X2,…,X9)是来自总体X 的简单随机样本,X是样本均值。考虑基本假设H0 的如下否定域![]() 本章中,除有特别说明外,uα 表示标准正态分布上侧α 分位数。试分别求检验的两类错误概率。
本章中,除有特别说明外,uα 表示标准正态分布上侧α 分位数。试分别求检验的两类错误概率。
解 由条件知H0:X~N(0,1),H1:X~N(1,1),样本容量n=9。当总体X~N(μ,σ2)时,有X~N(μ,σ2/n),因此H0:3X~N(0,1),H1:3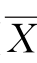 -1)~N(0,1)。
-1)~N(0,1)。
以![]() 为否定域的检验的两类错误概率α1 和β1 分别为
为否定域的检验的两类错误概率α1 和β1 分别为
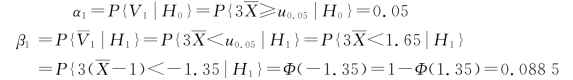
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




