【摘要】：在许多实际问题中,常常会遇到只需要求单侧的置信上限或下限的情况。若存在,对给定的α,有则称1为参数θ的置信度为1-α的单侧置信下限。例7.3.9 从一批灯泡中随机地取5只作寿命测试,测得寿命为设灯泡寿命服从正态分布,求灯泡寿命平均值的置信度为0.95的单侧置信下限。
在许多实际问题中,常常会遇到只需要求单侧的置信上限或下限的情况。如某品牌的冰箱,人们当然希望它的平均寿命越长越好,因此人们只关心这个品牌冰箱的平均寿命最低可能是多少,即关心平均寿命的下限。又如一批产品的次品率当然是越低越好,于是人们只关心次品率最高可能是多少,即关心次品率的上限。
定义7.3.2 设(X1,X2,…,Xn)为从总体X 中抽取的样本,θ为总体中的未知参数。若存在
,对给定的α(0＜α＜1),有
则称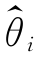
1为参数θ的置信度为1-α的单侧置信下限。若存在
,对给定的α(0＜α＜1),有
则称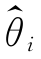
2为参数θ的置信度为1-α的单侧置信上限。
对于单侧置信区间估计问题的讨论,基本与双侧区间估计的方法相同,只是要注意对于精度的标准不能像双侧区间一样用置信区间的长度来刻画,此时对于给定的置信度1-α,选择置信下限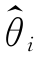
1,应该是E(
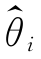1)越大越好,选择置信上限
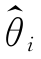2,应该是E(
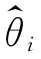2)越小越好。(www.xing528.com)
例7.3.9 从一批灯泡中随机地取5只作寿命测试,测得寿命(单位:小时)为
设灯泡寿命服从正态分布,求灯泡寿命平均值的置信度为0.95的单侧置信下限。
解 1-α=0.95,n=5,x=1160,s2=9950,t0.05(4)=2.1318,故
此即为灯泡寿命平均值的置信度为0.95的单侧置信下限。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
