两个正态总体均值之差与方差之比的区间估计-概率论与数理统计

在实际中,经常遇到以下问题:已知产品的某一质量指标服从正态分布,但由于原料、设备条件、操作人员不同,或工艺过程的改变等因素,使得总体均值、总体方差有所改变。我们需要知道这些变化有多大,这就需要考虑两个正态总体均值之差与方差之比的估计问题。

1.两个正态总体均值之差的区间估计

设有两个正态总体N(μ1,σ21)和N(μ2,σ22),分别从中抽取容量为n1 和n2 的样本,样本均值分别为X和Y,样本方差分别为S21 和S22,并设两个样本是互相独立的,下面就总体方差的不同情况来讨论μ1-μ2 的置信区间。

(1)总体方差σ21 和总体方差σ22 都已知

由的独立性以及知

从而有

把u 的表达式代入,得

故μ1-μ2 的置信区间是

(2)总体方差σ21 和总体方差σ22 未知,但已知σ21=σ22=σ2

由式(6.3.18)可知

两总体均值之差μ1-μ2 的置信区间是

此处

例7.3.4 为比较Ⅰ和Ⅱ两种型号步枪子弹的枪口速度,随机地取Ⅰ型子弹10发,得到枪口速度的平均值为,标准差为s1=1.10m/s,随机地取Ⅱ型子弹20发,得到枪口速度的平均值为=496m/s,标准差为s2=1.20m/s。假设两总体都可认为近似地服从正态分布,且由生产过程可认为方差相等,求两总体均值差μ1-μ2 的一个置信水平为0.95的置信区间。

解 按实际情况,可认为分别来自两个总体的样本是相互独立的,又因为假设两总体的方差相等,但数值未知,故可用式(7.3.7)求均值差的置信区间。由于1-α=0.95,=0.025,n1=10,n2=20,n1+n2-2=28,t0.025(28)=2.0484,s2w=(9×1.102+19×1.202)/28,sw=因此所求的两总体均值差μ1-μ2 的一个置信水平为0.95的置信区间是

例7.3.4中得到的置信区间的下限大于0,在实际中我们认为μ1 比μ2 大。(www.xing528.com)

例7.3.5 为提高某一化学过程的得率,试图采用一种新的催化剂,为慎重起见,在实验工厂先进行实验。设采用原来的催化剂进行了n1=8次试验,得到得率的平均值样本方差s21=3.89;又采用新的催化剂进行了n2=8次试验,得到得率的平均值,样本方差s22=4.02。假设两总体都可以认为服从正态分布,且方差相等,两样本独立,试求两总体均值差μ1-μ2 的置信水平为0.95的置信区间。

解 由题意可得

故可用式(7.3.7)求均值差的置信区间:

由于所得置信区间包含0,在实际中我们认为采用这两种催化剂所得的得率的均值没有显著差别。

2.两个正态总体方差之比的区间估计

设两个正态总体的分布分别是N(μ1,σ21)和N(μ2,σ22),其中μ1,μ2,σ21,σ22 都是未知的。从两个总体中独立地各取一个样本,样本方差分别记为S21 和S22。下面对两个总体方差之比作区间估计。

由定理6.3.1知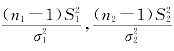分别服从自由度为n1-1和n2-1的χ2 分布,且S21 与S22 相互独立,由F 分布的定义知

并且F(n1-1,n2-1)分布不依赖任何未知参数。

即

故得的置信度为1-α的置信区间是:

方差之比的置信区间的含义是:若的置信上限小于1,则说明总体N(μ1,σ21)的波动性较小;若的置信下限大于1,则说明总体N(μ1,σ21)的波动性较大;若置信区间包含1,则难以从这次实验中判断两个总体波动性的大小,可以认为σ21=σ22。

例7.3.6 研究由机器A 和机器B生产的钢管的内径(单位:mm),随机抽取机器A 生产的管子18只,测得s21=0.34,抽取机器B生产的管子13只,测得s22=0.29,设两样本相互独立,且设由机器A、机器B生产的管子的内径分别服从正态分布N(μ1,σ21),N(μ2,σ22),其中μi,σ2i 均未知。试求方差比的置信水平为0.90的置信区间。

解 现在n1=18,s21=0.34,n2=13,s22=0.29,又α=0.10,查表得F0.05(17,12)=2.59,代入

得的置信水平为0.90的置信区间为(0.45,2.79)。