单一正态总体的均值与方差的区间估计

1.单一正态总体均值的区间估计

单一正态总体均值的区间估计一般分为两种情况:一是总体方差σ2 已知,求μ 的置信区间;二是总体方差σ2 未知,求μ 的置信区间。下面对这两种情况分别进行介绍。

(1)已知总体方差σ2,求均值μ 的置信区间

设(X1,X2,…,Xn)为总体X～N(μ,σ2)的一个样本,已知方差σ2=σ20,求μ的1-α置信区间。

根据定理,于是

记Φ(x)为N(0,1)的分布函数,Zα 为其上α 分位点,即Φ(Zα)=1-α,于是

等价于

这样我们就得到了μ 的置信系数为1-α的置信区间

例7.3.1 已知某工厂生产的某种零件的长度X～N(μ,0.06),现从某日生产的一批零件中随机抽取6只,测得长度(单位:mm)的数据为

14.6 15.1 14.9 14.8 15.2 15.1

试求该批零件长度的置信度为0.95的置信区间。

解 σ=经计算可得

当α=0.05时,查正态分布表可得,从而

故所求置信区间为(14.75,15.15)。

(2)总体方差σ2 未知,求均值μ 的置信区间

设(X1,X2,…,Xn)为总体X～N(μ,σ2)的一个样本,方差σ2 未知,求μ 的1-α置信区间。

由于σ2 未知,在这种情况下,应考虑用样本方差S2 来估计σ2。由定理6.3.2知

于是,利用t分布,可导出对正态总体均值μ 的区间估计。对于给定的α(0＜α＜1),使

即(www.xing528.com)

于是得到μ 的一个置信水平为1-α的置信区间

例7.3.2 有一大批糖果,现从中随机地取16袋,称得重量(单位:g)为

设袋装糖果的重量近似服从正态分布,试求总体均值μ 的置信水平为0.95的置信区间。

解 这里1-α=0.95,=0.025,n-1=15,t0.025(15)=2.1315,由给出的数据计算得x=503.75,s=6.2022。由式(7.3.2)得均值μ 的一个置信水平为0.95的置信区间为

2.单一正态总体方差的区间估计

(1)μ 已知时σ2 的置信区间

设(X1,X2,…,Xn)为来自正态总体N(μ,σ2)的一个样本,σ2 是未知参数,在μ 已知时,采用随机变量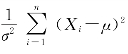 来构造σ2 的置信区间(可以证明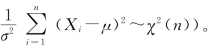

亦即

由此可得σ2 的置信度为1-α的置信区间为

(2)μ 未知时σ2 的置信区间

在μ 未知时,我们采用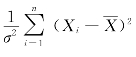 来构造σ2 的置信区间,此时

我们可以得到σ2 的置信度为1-α的置信区间为

其中

所以σ2 的置信度为1-α的置信区间为

例7.3.3 设高速公路上汽车的速度服从正态分布,现对汽车的速度独立地做了5次测试,求得这5次测试值的方差s2=0.09。求汽车速度的方差σ2 的置信度为0.9的置信区间。

解 由题意得n=5,1-α=0.9,α=0.1,查表得

算得

从而汽车速度的方差σ2 的置信度为0.9的置信区间为(0.038,0.506)。