【摘要】:定义7.2.2 设1 和2 是同一参数θ 的两个无偏估计量,若对于任意样本容量n 有D>D,则称2 较1 有效。例7.2.2 比较 的有效性,其中ai(i=1,2,…显然,当μ≠0时,μ 的任何线性无偏估计量必有例7.2.2中的1 的形式,所以例7.2.2也表明X是总体均值μ 的所有线性无偏估计量中最有效的一个,也就是说,样本均值是总体均值的最小方差无偏估计量。
既然参数θ的无偏估计不是唯一的,在θ的多个无偏估计之中就存在优劣问题,为此我们引入无偏估计量的有效性概念。
定义7.2.2 设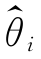 1 和
1 和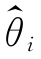 2 是同一参数θ 的两个无偏估计量,若对于任意样本容量n 有D(
2 是同一参数θ 的两个无偏估计量,若对于任意样本容量n 有D(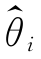 1)>D(
1)>D(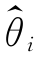 2),则称
2),则称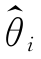 2 较
2 较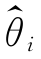 1 有效。
1 有效。
例如,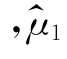 =X1 和
=X1 和 都是μ=E(X)的无偏估计量,由于
都是μ=E(X)的无偏估计量,由于
因此![]() 有效。从这个意义上讲,我们用
有效。从这个意义上讲,我们用![]() ,而不用
,而不用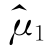 =X1 作为μ 的估计量。
=X1 作为μ 的估计量。
例7.2.2 比较![]() 的有效性,其中ai(i=1,2,…,n)为正常数,且
的有效性,其中ai(i=1,2,…,n)为正常数,且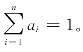
解 显然,当a1=a2=…=an=![]() 现设所有ai 不全相等。前面已证明X是总体均值μ 的无偏估计量,且计算得
现设所有ai 不全相等。前面已证明X是总体均值μ 的无偏估计量,且计算得![]() ,而
,而
利用不等式a2i+a2j≥2aiaj(当且仅当ai=aj 时等式成立)可得(https://www.xing528.com)
当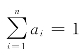 时,由上式可得
时,由上式可得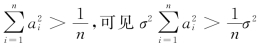 ,故
,故![]() 这表明,X比
这表明,X比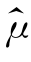 1 更有效。
1 更有效。
显然,当μ≠0时,μ 的任何线性无偏估计量必有例7.2.2中的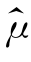 1 的形式,所以例7.2.2也表明X是总体均值μ 的所有线性无偏估计量中最有效的一个,也就是说,样本均值是总体均值的最小方差无偏估计量。
1 的形式,所以例7.2.2也表明X是总体均值μ 的所有线性无偏估计量中最有效的一个,也就是说,样本均值是总体均值的最小方差无偏估计量。
讨论和比较估计量的有效性时,研究最小方差无偏估计量是否存在以及存在的情况下如何寻找是一个比较复杂的问题,在这里不进行讨论,下面不加证明地给出两个结果:
①频率是概率的最小方差无偏估计量;
②对于正态总体N(μ,σ2),X和S2 分别是μ 和σ2 的最小方差无偏估计量。
由此我们不难理解,在实际工作中人们为什么将样本不合格率作为全部产品(总体)不合格率的估计量,用样本均值、样本方差分别作为总体均值、总体方差的估计量。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




