正态总体常用抽样分布

正态总体的统计推断在统计推断的理论和实际应用中占有特别重要的地位,凡是涉及正态总体的推断问题一般都有完满而简捷的结果。此外,正态总体的抽样分布一般都是精确分布。因此多数正态总体的统计推断方法并不要求样本容量充分大。

正态总体的抽样分布,主要是样本均值和样本方差的分布,所涉及的分布有:正态分布、χ2分布、t分布和F 分布。

1.样本均值和样本方差的分布

定理6.3.1 假设总体X ～N(μ,σ2)(X1,X2,…,Xn)是来自总体X 的简单随机样本,X和S2 相应为由式(6.2.1)定义的样本均值和样本方差。那么,

①样本均值X～N(μ,σ2/n),故

②随机变量

③样本均值X和样本方差S2 相互独立。

证明 证结论①。由于Xi ～N(μ,σ2)(i=1,2,…,n),且相互独立,故X作为独立正态随机变量的线性组合也服从正态分布,且E(X)=μ,D(X)=σ2/n。

结论②和③的证明略。

定理6.3.2 设(X1,X2,…,Xn)是来自总体N(μ,σ2)的样本,X,S2 分别是样本均值和样本方差,则有

证明 因为相互独立,于是根据t分布的定义有

即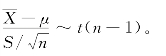

2.样本均值差和联合样本方差的分布

定理6.3.3 假设有两个总体X ～N(μ1,σ21)和Y ～N(μ2,σ22),且X 和Y 相互独立;(X1,X2,…,Xn1)是来自总体X 的简单随机样本,X 和S21 相应为其样本均值和样本方差;(Y1,Y2,…,Yn2)是来自总体Y 的简单随机样本,Y和S22 相应为其样本均值和样本方差。记

称作总体X 和Y 的联合样本方差。那么,以下命题成立。

①随机变量

②统计量 相互独立。

③若(记作σ2),则随机变量

④若σ21 =σ22,则随机变量

证明 (1)证命题①。因为独立正态随机变量的线性组合仍然服从正态分布,故X ～N(μ1,σ21/n1),Y～N(μ2,σ22/n2),所以X-Y也服从正态分布,其数学期望和方差为

命题①得证。

(2)证命题②。因为分别仅依赖于相互独立的两个样本,故它们相互独立;由于同一正态总体的样本均值和样本方差相互独立,可见X和S21 及Y和S22 各自相互独立。因此,对于任意实数t1,t2,t3,t4,有

从而相互独立。

(3)证命题③。由式(6.3.13)知

分别服从自由度为(n1-1)和(n2-1)的χ2 分布;而由命题②可见相互独立。因此,由χ2 分布的可加性知

服从χ2 分布,自由度为v= (n1-1)+(n2-1)=n1+n2-2。(www.xing528.com)

(4)证命题④。由命题②可见相互独立。易见,式(6.3.18)中的T 可以写成:

因此,由t分布随机变量的定义可见,随机变量T 服从自由度为v=n1+n2-2的t分布。

3.样本方差比的分布

定理6.3.4 假设有两个总体X ～N(μ1,σ21)和Y ～N(μ2,σ22),且X 和Y 相互独立。(X1,X2,…,Xn1)和(Y1,Y2,…,Yn2)分别是来自总体X 和Y 的简单随机样本,S21 和S22 分别相应为样本方差。那么,以下命题成立。

①随机变量

服从F (n1-1,n2-1)分布。

②如果 =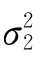,则两个样本方差之比

服从F (n1-1,n2-1)分布。

证明 命题②是命题①的特例,故只需证命题①。由式(6.3.19),有

由式(6.3.13)知服从自由度分别为n1-1,n2-1的χ2 分布。由两个样本的独立性可见S21 和S22 独立,从而 相互独立。由F 分布的定义,知式(6.3.19)中的F 服从F (n1-1,n2-1)分布。

例6.3.6 设总体Xi(i=1,2)服从正态分布N(μi,σi2),X1 和X2 独立。由来自总体Xi(i=1,2)的简单随机样本,得样本均值Xi 和样本方差Si2。证明:如果μ1 =μ2 =μ,则E(α1X1 +α2X2 )=μ,其中αi 是统计量:

证明 由于来自独立正态总体的相互独立,可见α1 和以及α2 和相互独立。从而有

例6.3.7 设X1,X2,…,X10 是来自正态总体X 的简单随机样本,

证明:统计量T 服从自由度为8的t分布。

证明 设X ～N(μ,σ2),则。易见

其中U ～N(0,1),随机变量χ2 服从自由度为8的χ2 分布。

现在证明U 和χ2 独立。事实上,对于正态总体,X和S2 独立;而由条件知X10 与(X,S2)独立。对于任意实数a,b,c,有

从而X10,X,S2 相互独立。因为U 仅依赖于(X10,X),而χ2 仅依赖于S2,所以U 和χ2 独立。于是,由式(6.2.1)知,统计量T 服从自由度为8的t分布。

4.样本均值极限抽样分布*

正态总体的抽样分布都是精确概率分布,适用于任何样本容量n。原则上,对于其他一些总体,用类似的方法也可以求出某些抽样分布,然而像正态总体那样有比较简捷和完满结果的却不多见。在类似的情况下,人们在样本容量充分大的情况下成功地使用极限分布。极限抽样分布的内容十分丰富,下面只准备介绍任意总体的样本均值的极限抽样分布是正态分布的情形。

设X 是任意总体,E(X)=μ,D(X)=σ2 存在。(X1,X2,…,Xn)是来自总体X 的简单随机样本,X和S2 相应为样本均值和样本方差,则当n充分大时

都近似服从标准正态分布。

证明 (1)由林德伯格-勒维定理,可见当n充分大时V 近似服从标准正态分布。

(2)证明略。