F分布在概率论与数理统计中的应用

定义6.3.3 设U ～χ2(n1),V ～χ2(n2),且U 与V 相互独立,则称随机变量

服从自由度为(n1,n2)的F 分布,记为F ～F(n1,n2)。可以证明,F(n1,n2)分布的概率密度函数为

F 分布曲线与χ2 分布曲线有类似的形状。ψ(y)的图形如图6.3.3所示。

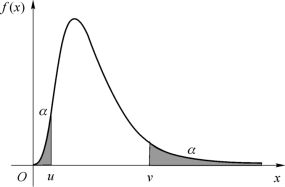
图6.3.3

F 分布具备如下一些性质。

①若F ～F(n1,n2),则～F(n2,n1)。

②若F ～F(n1,n2),则

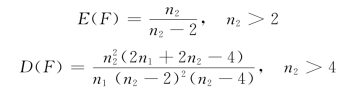
关于F 分布,我们也定义了分位数的概念并编制了相应的分位数值表(附表6)。(www.xing528.com)

F 分布的分位数:自由度为(n1,n2)的F 分布水平α 上侧分位数Fα(n1,n2)决定于

此时,F(n1,n2)表示服从自由度为(n1,n2)的F分布的随机变量。自由度为(n1,n2)的F分布水平α下侧分位数F1-α(n1,n2)决定于

对于不同的自由度(n1,n2)和α＜0.50,附表6是F 分布的上侧分位数的数值表。而对于α＞0.50,可以利用如下关系式求出分位数,

例如,由附表6可见,

例6.3.5 设随机变量X 和Y 都服从标准正态分布并且独立,求Z=X2/Y2 的概率分布。

解 由于X 和Y 都服从标准正态分布,可见X2 和Y2 都服从自由度为1的χ2 分布。此外,由X 和Y 独立,可见X2 和Y2 也独立。从而,由服从F 分布的随机变量的典型模式知随机变量Z=X2/Y2 服从自由度为(1,1)的F 分布。