t分布及其特点，与正态分布的近似关系

定义6.3.2 设X ～N(0,1),Y ～χ2(n),且X 与Y 相互独立,则称随机变量

服从自由度为n的t分布,记为T ～t(n)。可以证明,t(n)分布的概率密度函数为

h(t)的图形如图6.3.2所示。

图6.3.2

t分布密度h(t)曲线与标准正态分布密度φ(t)曲线非常接近。t分布有如下性质。

①t分布数字特征*

②t分布的极限分布

当自由度n→∞时,t分布的极限分布是标准正态分布,即有

实际应用中,当n≥30时即可用标准正态分布近似t分布。

③t分布的密度曲线

h(t)的图形关于纵轴对称。

④t分布的分位数

自由度为v的t分布水平α 上侧分位数tα(v)(附表4),决定于

自由度为v的t分布水平α 下侧分位数t1-α(v),决定于

(www.xing528.com)

由t分布的对称性,可知:

例6.3.3 假设总体X ～N(0,9),X1,X2,…,X8 是来自总体X 的简单随机样本,求统计量

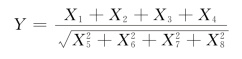
的概率分布。

解 由于独立正态分布的随机变量的和仍然服从正态分布,易见

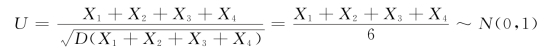
作为独立标准正态随机变量的平方和,

服从χ2(4)分布,随机变量U 和χ2 显然相互独立。随机变量Y 可以表示为

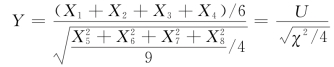
由t分布定义,可见随机变量Y 服从自由度为4的t分布。

例6.3.4 设随机变量X,Y1 和Y2 相互独立且都服从标准正态分布,求随机变量

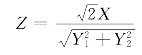
的概率分布。

解 由条件知X,Y1 和Y2 相互独立且都服从标准正态分布。随机变量作为两个独立标准正态随机变量的平方和,服从自由度为2的χ2 分布。因为

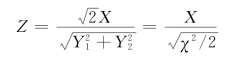
其中:X ～N(0,1),χ2 服从自由度为2的χ2 分布,X 和χ2=Y21+Y22 相互独立,所以由服从t分布的随机变量的典型模式知,随机变量Z 服从自由度为2的t分布。