概率论与数理统计节：χ2分布

定义6.3.1 若一个随机变量X 的概率密度为^[2]

称X 服从自由度为v的χ2 分布,记作X ～χ2(v)。χ2 分布密度曲线(k=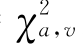)如图6.3.1所示。

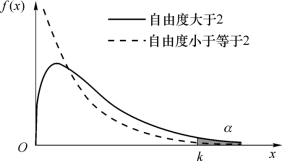
图6.3.1

(1)χ2 变量的典型模式

可以证明,独立的标准正态随机变量的平方和服从χ2 分布。即,若U1,U2,…,Un 是相互独立的随机变量,且Ui ～N(0,1),i=1,2…,n,则随机变量

服从自由度为n的χ2 分布。自由度n恰好是构成变量X 的标准正态随机变量的个数。

由上述结论易知:若X1,X2,…,Xn 是来自总体N(0,1)的样本,则统计量

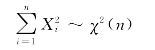
例6.3.1 设X1,X2,X3,X4,X5 是来自正态总体N(0,4)的简单随机样本,记

问当a,b,c各取何值时,统计量T 服从χ2 分布,其自由度如何?

解 由条件知X1,X2,…,X5 相互独立且同正态分布N(0,4),因此

且相互独立。由式(6.3.2)知

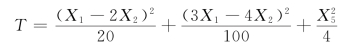
服从自由度为3的χ2 分布,从而

(2)χ2 分布的数字特征

χ2 分布的数字特征为E(X)=n,D(X)=2n。(www.xing528.com)

证明见例6.3.2。

例6.3.2 假设随机变量X 服从自由度为n 的χ2 分布,求E(X)和D(X)。

解 设U1,U2,…,Un 是独立标准正态分布随机变量,则服从自由度为n的χ2 分布的随机变量X 可以表示为

由于Ui ～N(0,1),可见E(Ui)=0,D(Ui)=E(U2i)=1(i=1,2,…,n),

由上式可见E(X)=n,

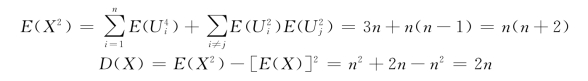
于是E(X)=n,D(X)=2n。

(3)χ2 变量的可加性

若χ21,χ22,…,χ2m 相互独立,且都服从χ2 分布,自由度相应为n1,n2,…,nm,则

服从自由度为n=n1+n2+…+nm 的χ2 分布。

证明 由式(6.3.2)知,χ2 =χ21+χ22+…+χ2m 可以表示为n=n1+n2+…+nm 个标准正态变量的平方和,故服从自由度为n=n1+n2+…+nm 的χ2 分布。

(4)χ2 分布的分位数

统计推断常要用到χ2 分布的上侧分位数。以χ2α(v)表示自由度为v的χ2 分布水平为α(0＜α＜1)的上侧分位数(图6.3.1),它决定于如下等式:

附表5是上侧分位数χ2α(v)的数值表。例如

对应地,我们还经常用到χ2 分布的下侧分位数。借助上侧分位数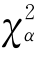(v)的记号,则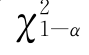(v)表示自由度为v的χ2 分布水平为α(0,1)的下侧分位数,它满足于如下等式: