中心极限定理及其推广

通过实践人们发现,如果一个量是由大量相互独立的随机因素综合作用的结果,而每一个随机因素在总的结果中所起的作用又非常微小,则这个量通常都服从或近似服从正态分布。正态分布在随机变量的各种分布中,占有极其重要的地位,自从德国数学家高斯指出测量误差服从正态分布后,人们发现,正态分布在自然界中极为常见。例如,炮弹的弹着点服从正态分布,人的许多生理特征诸如身高、体重等也服从正态分布。在某些条件下,即使原来并不服从正态分布的一些独立的随机变量,它们的和的分布,当随机变量的个数无限增加时,也是趋于正态分布的。在概率论中,中心极限定理研究独立随机变量的前n项和在什么条件下近似服从正态分布。这些内容奠定了数理统计中有关大样本的理论基础。

定义5.3.1 若对于独立随机变量序列ξ1,ξ2,…,ξn,… 的前n 项标准化和ηn =成立,则称随机变量序列ξn｛ ｝服从中心极限定理(TheCentralLimitTheorem)。

该定义表明,对于满足条件的随机变量序列ξ1,ξ2,…,ξn,… 的前n 项标准化和有结论ηn服从或近似服从N(0,1)时,可以推出服从或近似服从,每个前n项标准化和随机变量ηn 对应一个分布函数Fn(x),这就得到了分布函数序列,中心极限定理的结论描述的正是分布函数序列{Fn(x)=P{ηn ≤x}}收敛于标准正态分布的各种情况。

下面简单介绍3个常见的中心极限定理。

定理5.3.1 设随机变量ξ1,ξ2,…,ξn,…相互独立,服从同一分布,且具有相同的数学期望和方差:E(ξk)=μ,D(ξk)=σ2≠0(k=1,2,…),那么,对于随机变量序列前n 项标准化和ηn的极限恒成立下式

其中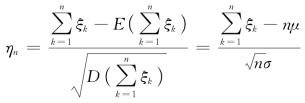,定理5.3.1称为林德伯格-勒维(Lindeberg-Levy)中心极限定理,也称为独立同分布的中心极限定理。

证明略。

独立同分布的中心极限定理在实践中非常重要并且有着非常广泛的应用。例如,多次重复观测结果ξ1,ξ2,…,ξn 的算术平均值ξn 近似服从正态分布。

再例如,只要n足够大,就可以把独立同分布的随机变量之和当作正态随机变量来处理。这种做法在数理统计中使用得非常普遍,当处理大样本问题时,它将作为一个非常重要的理论工具。

在概率论历史上,有关中心极限定理的研究最初来源于伯努利试验,而后才被推广到比较一般的场合。Lindeberg-Levy中心极限定理正是这许多推广之一,它所描述的独立同分布场合是数理统计中最常见的情形。

例5.3.1 由均匀分布可以得到正态分布的近似。

假设随机变量ξ1,ξ2,…,ξn 独立,且都在区间[0,1]上服从均匀分布),则由Lindeberg-Levy中心极限定理知,当n 充分大时Sn=ξ1+ξ2+…+ξn近似地服从正态分布从而近似地

而对于任意μ 和σ＞0,近似地

特别地,当n=12时,得

如果将上式中的ξ1,ξ2,…,ξ12分别换成区间[0,1]上的均匀随机数,则得一个(近似的)标准正态随机数(可视为对标准正态分布随机变量的一次观测所取得的数值),当n=1200时,公式变为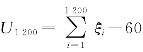,该公式的近似效果会更好。

有兴趣的读者可以使用计算机产生区间[0,1]上的均匀随机数从而得到一系列的标准正态随机数(严格地说这些是伪随机数,它们具备正态随机变量的性质但不是通过物理发生器获得的)。

例5.3.2 一生产线上加工成箱零件,每箱平均重50kg,标准差为5kg。假设承运这批产品的汽车的最大载重量为5吨,试利用中心极限定理说明该车最多可以装多少箱,才能以概率97.7%保障不超载?

解 以ξi(i=1,2,…,n)表示装运的第i箱产品的实际重量,n 为所求箱数。由条件可以认为随机变量ξ1,ξ2,…,ξn 独立同分布,因而总重量Tn=ξ1+ξ2+…+ξn 是独立同分布随机变量之和。由条件,有E(ξi)=50,σ=因而E(Tn)=50n,(单位:千克)。

随机变量ξ1,ξ2,…,ξn 独立同分布且具有相同的数学期望和方差,根据独立同分布中心极限定理,只要n 充分大,随机变量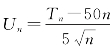就近似服从标准正态分布N(0,1)。由题意知,所求n应满足条件

查阅标准正态分布表,得到P｛ Un≤2｝≥0.977。从而有

经试算,对于n=97,an=3.05;对于n=98,an=2.02;对于n=99,an=1.01;由此可见应取n=98,即最多只能装98箱。

定理5.3.2 设随机变量ξ1,ξ2,…,ξn,…相互独立,且

记

若存在δ＞0,使当n→∞时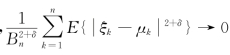,则恒成立

定理5.3.2称为李雅普诺夫(Liapunov)中心极限定理。

证明略。

上述定理表明,在相当广泛的情形下,无论随机变量ξk 服从怎样的分布,只要n 充分大,那么它们的和就近似地服从正态分布。这就是正态分布是实际问题中最常见的一种分布,以及正态分布在概率论中占有非常重要地位的基本原因。同时也从理论上揭示了正态分布的形成机制:如果某一个量的变化是大量微小的、相互独立的随机因素综合作用的结果,而且这些随机因素中没有任何一个是起主导作用的,那么,这个量就是一个服从正态分布的随机变量,至少它近似地服从正态分布。这种机制在经济问题中是常见的,当我们对一些经济问题进行定量分析时,往往假定在主要因素的影响外,其他各种因素的影响可以用一个服从正态分布的随机变量来表示,其根据即在于此。

定理5.3.3 若｛nA｝是随机变量序列,且nA～B(n,p)(n=1,2,…),记ηn=则恒成立(www.xing528.com)

定理5.3.3称为棣莫弗-拉普拉斯(DeMoivre-Laplace)中心极限定理。

证明 因为nA～B(n,p),所以nA 表示n 重伯努利试验中事件A 出现的次数。定义

则有nA=ξ1+ξ2+…+ξn。由于ξ1,ξ2,…,ξn,…相互独立,都服从0-1分布,且有E(ξk)=p,D(ξk)=p(1-p),因为ξ1,ξ2,…,ξn,…前n项随机变量的标准化和为

即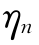 就是前n 项随机变量的标准化和,所以应用Lindeberg-levy中心极限定理有:

这个定理便是伯努利试验场合下的中心极限定理。关于这一古典结果在各种场合下的推广,构成了我们所研究的一系列中心极限定理。

上述定理的结果表明,二项分布的极限分布是正态分布。因此,当n 充分大时,若随机变量nA～B(n,p),则近似地有nA～N(np,np(1-p)),于是可以利用正态分布近似地计算形如P{a＜nA≤b}的概率。事实上,若记np=μ,np(1-p)=σ2,则有

这就是部分积分定理的一种表达式,事实上当n充分大时,还可以近似计算

这就是局部极限定理的一种表达式。

在这里,顺便澄清一个概念。在前面章节的讨论中,我们曾学习过二项分布的泊松逼近。当时,泊松分布虽然作为二项分布的极限分布引入的,但极限过程强调的是:n→∞时,pn 逐渐减小,而npn→λ,而“二项分布的极限分布是正态分布”这一结论强调的极限过程是:n→∞时,p 是常数,二者是有区别的,在运用时要加以区别才能取得更好的近似效果。

例5.3.3 在一家保险公司里有10000人参加人寿保险,每人每年交保费12元,假定一年内一个人意外死亡的概率为0.0006,死亡时其家属可向保险公司索赔10000元,问:

(1)保险公司亏本的概率有多大?

(2)保险公司一年的利润不低于40000元的概率有多大?

解 以ξ记10000个参加保险的人中一年内意外死亡的人数,则ξ～B(10000,0.0006)。因此,P{10000ξ＞120000}表示保险公司亏本的概率,P{120000-10000ξ≥40000}表示保险公司一年的利润不低于40000元的概率。由于n=10000比较大,所以根据DeMoivre-Laplace中心极限定理得:

例5.3.4 假设在某保险公司的索赔户中因被盗索赔者占20%。试求在200个索赔户中因被盗而索赔的户数ξ介于25户和55户的概率α。

解 易见,随机变量ξ服从二项分布,参数为n=200,p=0.20,其数学期望和方差为

由于n充分大,故根据DeMoivre-Laplace中心极限定理,近似地

于是,因被盗而索赔的户数介于25户和55户的概率为

例5.3.5 某车间有同型号机床200台,每台开动的概率为0.7,假定各机床开动与否是相互独立的,开动时每台机床耗电15个单位,问:最少要供应这个车间多少电能,才能以不低于95%的概率保证不致因电力不足而影响生产。

解 以η记200台机床中同时开动的台数,则有η～B(200,0.7)。设最少要供应m 台机床同时开动所需的电能,才能以不低于95%的概率保证不致因电力不足而影响生产。于是P｛ η≤m｝≥0.95。应用DeMoivre-Laplace中心极限定理(此时认为n=200比较大)有

查正态分布表得

所以m≥151。

这样便求得,最少要供应这个车间15×151=2265个单位的电能,才能以不低于95%的概率保证不致因电力不足而影响生产。

第1章人们基于长期的实践认识到频率具有稳定性,也就是说随着试验次数的不断增多,频率的波动越来越小并且稳定在常数附近。这说明事件发生可能性的大小可以用这个常数来表示,进而由频率的性质引出并抽象了概率的概念,这说明频率的稳定性是概率这个概念客观存在的基础,但前面几章并没有给出频率稳定性这一事实的严格数学证明,本章伯努利大数定律以严格的数学形式给出了频率稳定性的证明,并且还指出在一定条件下,随机变量前n项的算术平均值也具有稳定性,不同的条件构成了一系列的大数定律的内容,除伯努利大数定律外,还简单介绍了切比雪夫大数定律及辛钦大数定律。

随着随机变量个数的增加并且趋向于无穷大时,由这些随机变量和构成的新随机变量分布函数具有正态分布的良好性质(自从德国数学家高斯指出测量误差服从正态分布之后,正态分布在概率论中就具有了非常重要的地位),因为这类问题研究中突出了中心化、标准化、极限化,它又是数理统计中大样本的理论基础,因此波利亚(Polya)给这类定理取名为中心极限定理。

中心极限定理揭示了在相当一般的条件下,随着独立随机变量个数的增加,其和的分布趋于正态分布,这在实践中经常遇到,同时也说明正态分布时时处处存在的根源,并详细证明了独立同分布随机变量在方差存在的情况下(不管随机变量服从什么分布),其和随着随机变量个数的增加正态分布的逼近效果越来越好,这在实践上的意义充分得到体现。

随机变量标准化和的分布函数序列的极限分布的证明过程就是从数学上严格论证了中心极限定理,本章介绍了常用的3个中心极限定理:林德伯格-勒维中心极限定理、李雅普诺夫中心极限定理、棣莫弗-拉普拉斯中心极限定理,这解决了独立同分布方差存在的随机变量序列和、0-1分布序列和(二项分布)等一系列和的极限分布是正态分布的问题,为实践应用奠定了坚实的理论基础。