方差性质分析：概率论与数理统计书籍

方差有以下3条性质:

①设c是常数,则D(c)=0;

②设X 是随机变量,a是常数,则有

③设X,Y 是两个相互独立的随机变量,则有

证明

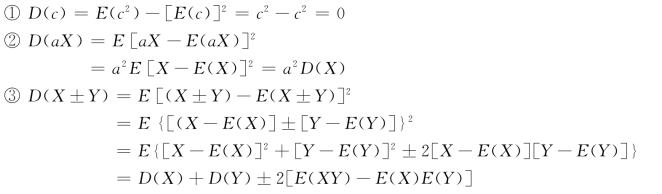
由于X,Y 相互独立,由数学期望的性质④知

故得

例4.2.3 设Y ～B(n,p),求D(Y)。

解 设Y=X1+X2+…+Xn,其中X1,X2,…,Xn 相互独立,且都服从参数p的0-1分布,由方差的性质③推广得

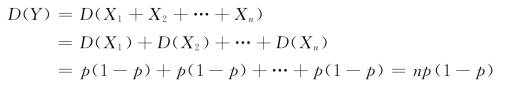
例4.2.4 对目标进行射击,直到击中目标为止。如果每次射击的命中率为p,求射击次数X 的数学期望和方差。

解 由题意可求得X 的分布律为

于是

由于

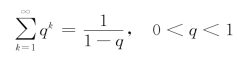
对此级数逐项求导,得

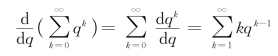
因此

从而

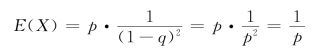(www.xing528.com)

为了求D(X),先求E(X2)。由于

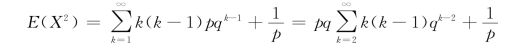
注意到

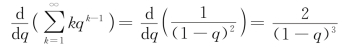
从而

因此

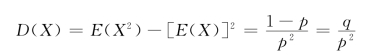
例4.2.5 袋中有n张卡片,编号为1,2,…,n,从中有放回地抽出k张卡片,求所得号码之和的方差。

解 设ξi 是第i次抽得的卡片号码,因为抽样是有放回的,所以ξ1,ξ2,…,ξk 相互独立,按方差的性质,有

易知ξi 的分布列是

从而

所以

例4.2.6 设X ～N(μ,σ2),求D(X)。

解 令Y =,则Y ～N(0,1),

可见,σ2 是X ～N(μ,σ2)的方差,从N(μ,σ2)的概率密度f(x)的图形(图4.2.1)可以看出,当σ2 较小时,f(x)的图形“高而瘦”,这说明,方差较小时,X 与E(X)的偏差较小,即X 取值的集中度较高;当σ2 较大时,f(x)的图形“低而胖”,说明方差较大时,X 相对于E(X)的偏差较大,即X 的取值的分散度较高。

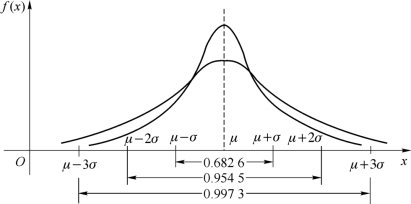
图4.2.1

因此,方差实质上完整地反映了变量X 取值的散布状况。关于X ～N(μ,σ2),下面指出3个重要数据(图4.2.1)。

最后这个式子说明,X 的值落在[μ-3σ,μ+3σ]上的概率几乎为1,这一事实称为“3σ法则”。