数学期望有以下4条性质:
①设c是常数,则有E(c)=c;
②设X 是一个随机变量,c是常数,则有E(cX)=cE(X);
③设X,Y 是两个随机变量,则有E(X+Y)=E(X)+E(Y);
④设X,Y 是相互独立的随机变量,则有E(XY)=E(X)E(Y)。
证明 (仅就连续型给出证明,离散型的证明类似)设随机变量X 的概率密度为f(x),数学期望为E(X),则对于任意的常数a,b,有

取a=0,b=c即得①;取b=0,a=c即得②。
设二维随机变量(X,Y)的联合概率密度为f(x,y),则

又若(X,Y)的边缘概率密度分别为fX(x),fY(y),X,Y 相互独立,则有
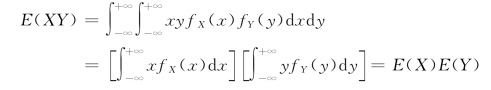
例4.1.10 r个人在楼的底层进入电梯,楼上有n层,每个乘客在任一层下电梯的概率相同。如果某一层无乘客下电梯,电梯就不停,求直到乘客都下完时电梯停的次数X 的数学期望。
解 设Xi表示在第i层电梯停的次数。则

易见,
由于每个人在任一层下电梯的概率均为![]() 故r 个人同时不在第i 层下电梯的概率为
故r 个人同时不在第i 层下电梯的概率为![]() 。即
。即
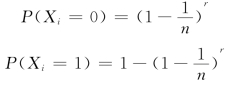
于是,
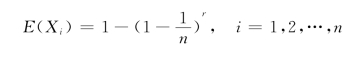
故
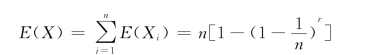 (https://www.xing528.com)
(https://www.xing528.com)
例4.1.11 设随机变量Y ~B(n,p),求E(Y)。
解 设Y=X1+X2+…+Xn,其中,X1,X2,…,Xn 相互独立,且每个都服从参数为p的0-1分布,由性质③的推广得
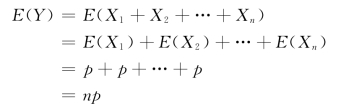
例4.1.12 假设随机变量Y 服从参数为λ=1的指数分布,随机变量
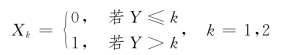
求:(1)X1 和X2 的联合概率分布;(2)E(X1+X2)。
解 显然,Y 的分布函数为
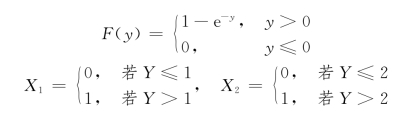
(1)(X1+X2)有4个可能取值:(0,0),(0,1),(1,0),(1,1),且

于是X1 和X2 的联合分布律如表4.1.2所示。
表4.1.2
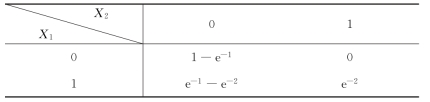
(2)显然,X1,X2 的分布律分别为
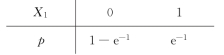

因此
![]()
故
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




