随机变量函数期望的计算方法概率论与数理统计

1.一维随机变量函数的期望

定理4.1.1 设Y 是随机变量X 的函数,Y=g(X)(g(x)是连续函数)。

①若X 是离散型随机变量,其分布律为

且级数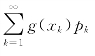收敛,则

②若X 是连续型随机变量,其分布密度为f(x),且积分 收敛,则

从公式可以看出:当求E[g(X)]时,不必知道g(X)的分布,只需知道X 的分布就可以了。这给求随机变量函数的期望带来很大方便。

例4.1.5 已知随机变量X 的分布律为

求:(1)E(X);(2)E(X2);(3)E(2X+3)。

解 (1)由式(4.1.1)得

(2)由式(4.1.3)得

(3)同理,得

例4.1.6 一辆汽车沿街道行使,需要通过3个相互独立的红绿信号灯路口,已知红绿信号显示时间相等,以X 表示该汽车首次遇到红灯时已通过的路口个数,求

解 X 的可能取值为0,1,2,3。记Ai={汽车在第i 个路口首次遇到红灯},则P(Ai)=

例4.1.7 已知随机变量X 在［0,2π］上服从均匀分布,求E(sinX)。

解 由题意知X 的分布密度为

由式(4.1.2)得

例4.1.8 按节气出售的某种节令商品,每售出1千克可获利a 元,过了节气处理剩余的这种商品,每售出1千克净亏损b元。设某店在季度内这种商品的销售量X 是一随机变量,X在区间(t1,t2)内服从均匀分布。问该店应进多少货才能使销售利润的数学期望最大?(www.xing528.com)

解 设t(单位:千克)为进货数,t1≤t≤t2,进货数t所获利润记为Y,则Y 是随机变量,

由于X 的概率密度为

因此

令

得驻点

由此可知,该店应进千克商品才可以使利润的数学期望最大。

2.二维随机变量函数的期望

定理4.1.2 设Z 是随机变量X,Y 的函数:Z=g(X,Y)(g 是连续函数)。若(X,Y)是二维离散型随机变量,分布律为

则有

若(X,Y)是连续型随机变量,其概率密度为f(x,y),则

证明略。

作为特例,在此定理中取g(X,Y)=X,则得E(X);取g(X,Y)=Y,则得E(Y)。

例4.1.9 设二维随机变量(X,Y)的概率密度为

求E(X),E(Y),E(XY)。

解

由X,Y 的取值和f(x,y)的对称性,得E(Y)=