对于随机变量,时常要考虑它的平均取值。先来看一个例子:经过长期观察积累,某射手在每次射击中命中的环数X 服从分布:

(其中0表示脱靶)
一种很自然的考虑是:假定该射击手进行了100次射击,那么,约有5次命中5环,5次命中6环,10次命中7环,10次命中8环,20次命中9环,50次命中10环,没有脱靶的。从而在一次射击中,该射手平均命中的环数为
![]()
它是X 的可能取值与对应概率的乘积之和。由此引出如下定义。
定义4.1.1 设离散型随机变量X 的分布律为

若级数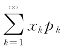 收敛,则称级数
收敛,则称级数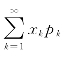 为随机变量X 的数学期望,简称期望或均值,记作E(X),即
为随机变量X 的数学期望,简称期望或均值,记作E(X),即
![]()
例4.1.1 设随机变量X 表示掷一颗骰子出现的点数,则X 的分布律为

求随机变量X 的数学期望。
解 E(X)=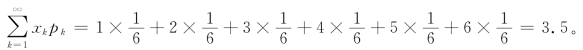
例4.1.2 设有两种投资方案,它们获取的利润如表4.1.1所示。
表4.1.1

试比较两种投资方案哪种较好。
解 设X 表示甲方案所获取的利润,Y 表示乙方案所获取的利润。则它们的分布律分别为


要比较甲、乙两种投资方案的优劣,也就是要比较两种方案谁获得的平均利润高,于是有
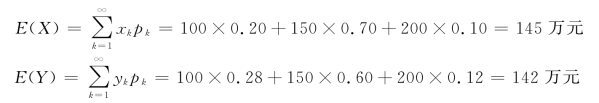
计算结果表明:甲方案略好于乙方案。
例4.1.3 设一台机器一天内发生故障的概率为0.2,机器发生故障时全天停工。若一周5个工作日里无故障,可获利10万元;发生一次故障获利5万元;发生2次故障获利0元,发生3次或3次以上故障亏损2万元,求一周内期望利润是多少?
解 设X 表示一周5个工作日内机器发生故障的天数,则X~B(5,0.2);设Y 表示一周内所获利润,则P(Y=10)=P(X=0)=(1-0.2)5=0.328。
同理可得Y 的分布律为

于是E(Y)=5.216万元。
例4.1.4 设随机变量X 具有如下的分布,
![]()
求E(X)。
解 因为
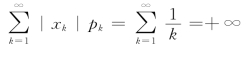
所以,E(X)不存在。
一些常用离散型随机变量分布的数学期望如下。
1.0-1分布
设随机变量X 服从0-1分布,其分布律为
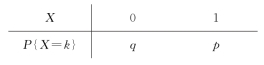
![]() (https://www.xing528.com)
(https://www.xing528.com)
由式(4.1.1)得
![]()
2.二项分布
设随机变量X~B(n,p),其分布律为
![]()
由式(4.1.1)得

3.泊松分布
设随机变量X~π(λ),其分布律为
![]()
由式(4.1.1)得

已知离散型随机变量X 的数学期望为E(X)=![]()
设X 是连续型随机变量,密度函数为f(x),用离散化的方式加以解释,如图4.1.1所示,在数轴上取很密的分点x0<x1<x2<…,阴影面积近似为f(xi)Δxi,则X 落在小区间(xi,xi+1)的概率为


图4.1.1
类推得Y 的数学期望为
定义4.1.2 设连续型随机变量X 的分布密度为f(x),如果积分![]() 由微积分知识自然想到X 的数学期望为
由微积分知识自然想到X 的数学期望为![]() 收敛,则称
收敛,则称![]() 为随机变量X 的数学期望,简称期望或均值,记作E(X),即
为随机变量X 的数学期望,简称期望或均值,记作E(X),即
![]()
一些常用连续型随机变量分布的数学期望如下。
1.均匀分布
设随机变量X 在[a,b]上服从均匀分布,其分布密度为
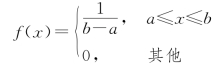
由式(4.1.2)得
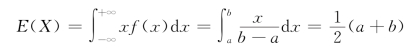
2.指数分布
设随机变量X 服从指数分布,其分布密度为
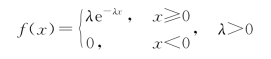
由式(4.1.2)得

3.正态分布
设随机变量X~N(μ,σ2),其分布密度为

由式(4.1.2)得
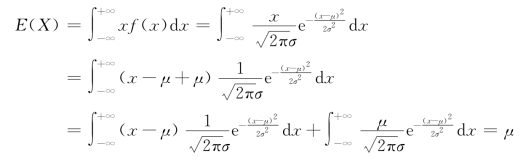
特别地,若随机变量X~N(0,1),则
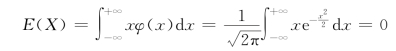
这是因为被积函数在(-∞,+∞)内是奇函数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




