同第2章一样,现在介绍求两个或两个以上随机变量函数的概率分布的方法。以二维随机变量来说明:即,设z=g(x,y)为二元实函数,求新的随机变量Z=g(X,Y)的分布,本节将重点介绍一些较简单且常用的情形。
1.一般情形
已知二维随机变量(X,Y)的概率分布(如联合分布函数,或联合密度,或联合分布律),而随机变量Z 为X 与Y 的函数,即Z=g(X,Y),则Z 的分布函数为
![]()
2.离散型情形
已知P{X=xi,Y=yj}=pij,Z=g(X,Y),则Z 的分布律为
![]()
3.连续型情形
已知(X,Y)~f(x,y),Z=g(X,Y),则Z 的分布函数为
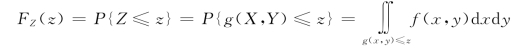
若Z 仍为连续型随机变量,则Z 的密度函数为
![]()
实际上,Z=g(X,Y)可能是离散型的或奇异型的,如Z=g(X,Y)=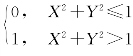 就是离散型的。
就是离散型的。
4.特殊型
(1)和的分布
设(X,Y)~f(x,y),则Z=X+Y 的密度函数为
![]()
当X 与Y 独立时,有卷积公式:
![]()
证明 对任意实数z,记G={(x,y):x+y≤z}为平面区域(图3.5.1)。先求Z=X+Y的分布函数:令x=u-y,得
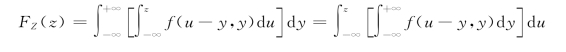
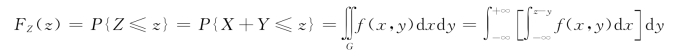
求导,得

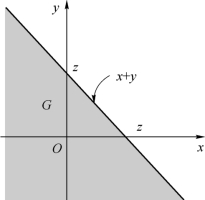
图3.5.1
类似可得两个连续型随机变量之差、积、商的概率密度公式。如商的分布:
设(X,Y)~f(x,y),则Z=![]() 的密度函数为
的密度函数为
![]()
当X 与Y 独立时,有
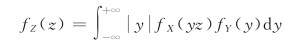
(2)极值分布
设X 与Y 相互独立,其分布函数分别为FX(x),FY(y),则Z1=max(X,Y),Z2=min(X,Y)的分布函数为
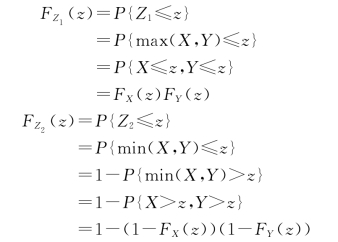
显然,上述结果可推广到n个相互独立的随机变量X1,X2,…,Xn,此时有
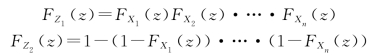
其中![]()
例3.5.1 设X 和Y 分别服从参数为λ1 和λ2 的泊松分布,并且相互独立,证明X+Y 服从参数为λ1+λ2 的泊松分布。
证明 由条件知

对于任意自然数n,有(https://www.xing528.com)
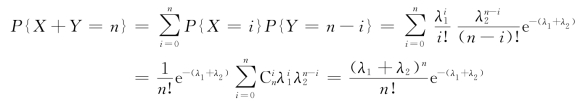
从而,X+Y 服从参数为λ1+λ2 的泊松分布。
注意
本题反映了泊松分布具有可加性,类似的还有:
①若X~B(m,p),Y~B(n,p),且X 与Y 相互独立,则X+Y~B(m+n,p);
②若X~N(μ1,σ21),Y~N(μ2,σ22),且X 与Y 相互独立,则X+Y~N(μ1+μ2,σ21+σ22)。
例3.5.2 假设随机变量X~N(0,1),求Y=max{X,X3}的概率密度f(y)。
解 随机变量Y=max{X,X3}的分布函数为
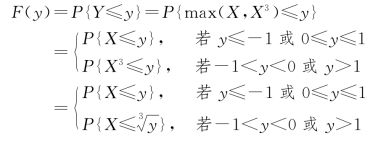
于是,随机变量Y=max{X,X3}的概率密度为
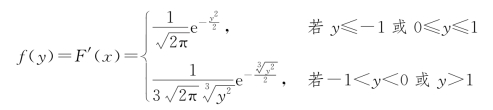
例3.5.3 假设随机变量(X,Y)在以点(0,1),(1,0),(1,1)为顶点的三角形区域上服从均匀分布。试求随机变量Z=X+Y 的概率密度f(z)。
解 G={(x,y):0≤x≤1,0≤y≤1;x+y≥1}是以点(0,1),(1,0),(1,1)为顶点的三角形区域,其面积等于![]() 随机变量(X,Y)的概率密度为
随机变量(X,Y)的概率密度为

显然,当z<1或z>2时,f(z)=0,设1≤z≤2。只有当0≤x≤1且0≤z-x≤1时,即当0≤z-1≤x<1时f(x,z-x)=2,否则f(x,z-x)=0,故有
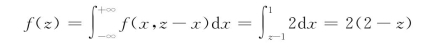
于是,随机变量Z=X+Y 的概率密度为
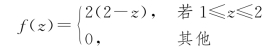
注:读者还可利用先求分布函数的方法求得。
例3.5.4 假设连续型随机变量(X,Y)在矩形G={(x,y):0≤x≤2,0≤y≤1}上的密度为常数,而矩形G 之外为0。求边长为X 和Y 的矩形面积S=XY 的概率分布。
解 随机变量(X,Y)的概率密度为
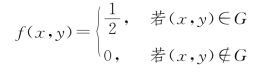
设F(s)为S=XY 的分布函数,则当s≤0时,F(s)=0;当s≥2时,F(s)=1。对于0<s<2,曲线xy=s(0<x<2)将矩形
![]()
分为两部分(图3.5.2):曲线的上方xy>s和曲线的下方xy<s;曲线xy=s(0<x<2)与矩形上方的边的交点为(s,1)。于是,对于0<s<2,有
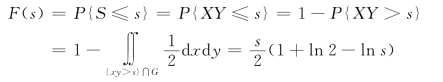
最后,得S 的概率密度为
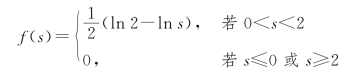
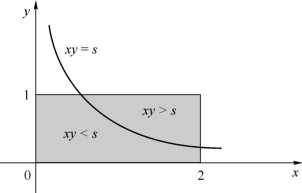
图3.5.2
例3.5.5 设随机变量X,Y 相互独立,X 的概率分布为P{X=i}=![]() (i=-1,0,1),Y 的概率密度为
(i=-1,0,1),Y 的概率密度为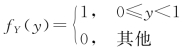 ,记Z=X+Y,求:
,记Z=X+Y,求:
(1)![]()
(2)Z 的概率密度fZ(z)。
解 (1)由于X,Y 相互独立,于是
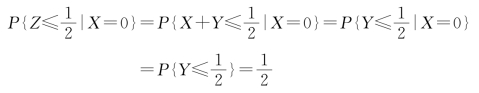
(2)先求Z 的分布函数。由于{X=-1},{X=0},{X=1}构成一个完备事件组,因此根据全概率公式得Z 的分布函数
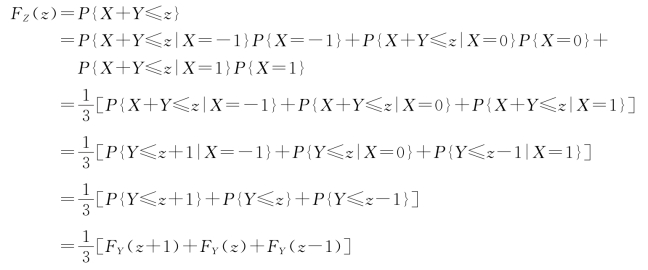
FY(z)表示Y 的分布函数。
于是Z 的密度函数为
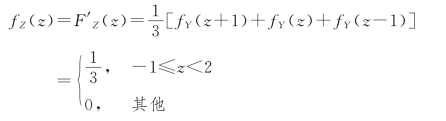
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




