与一维情形类似,二维连续型随机变量的概率分布,通过一个非负二元函数——联合密度的积分表示。
定义3.3.1 若存在非负可积函数f(x,y),使对任意的x,y,二维随机变量(X,Y)的分布函数都可表示为 则称(X,Y)是二维连续型随机变量,而f(x,y)称为(X,Y)的概率密度(或密度函数、分布密度),也称为X 与Y 的联合概率密度。
则称(X,Y)是二维连续型随机变量,而f(x,y)称为(X,Y)的概率密度(或密度函数、分布密度),也称为X 与Y 的联合概率密度。
二维随机变量的概率密度有如下性质。
①f(x,y)≥0。
②![]()
③在f(x,y)的连续点处,有![]()
④对xOy 面上的区域G,有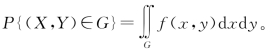
性质①是定义的要求。性质②由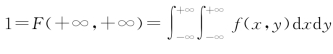 即得,此性质说明,在几何上介于xOy 面与概率密度曲面z=f(x,y)之间的曲顶柱体的体积为1;在物理上,若把f(x,y)看作面密度,则F(x,y)即为质量,这也是f(x,y)叫作概率密度的原因。性质③利用变限积分的求导法则直接可得。性质④借助于物理意义很容易理解。
即得,此性质说明,在几何上介于xOy 面与概率密度曲面z=f(x,y)之间的曲顶柱体的体积为1;在物理上,若把f(x,y)看作面密度,则F(x,y)即为质量,这也是f(x,y)叫作概率密度的原因。性质③利用变限积分的求导法则直接可得。性质④借助于物理意义很容易理解。
另外,若有一个二元实函数f(x,y)满足上述性质①及性质②,则f(x,y)一定是某一个二维连续型随机变量的概率密度。
定义3.3.2 设(X,Y)为二维连续型随机变量,称X(或Y)的概率密度为(X,Y)关于X(或Y)的边缘概率密度。
对于连续型随机变量(X,Y),设其联合概率密度为f(x,y),则由
![]()
可知,X 的概率密度为
![]()
同样,Y 也是连续型随机变量,且概率密度为
![]()
定义3.3.3 设(X,Y)为二维连续型随机变量,其联合概率密度为f(x,y)。对固定的y,若fY(y)>0,则称![]() 为在Y=y 条件下随机变量X 的条件概率密度,记作fX|Y(x|y)。
为在Y=y 条件下随机变量X 的条件概率密度,记作fX|Y(x|y)。
当fX(x)>0 时,同样有在X=x 条件下随机变量Y 的条件概率密度fY|X(y|x)=![]()
由定义3.3.3可看出,与概率密度一样,条件概率密度也满足如下两个基本条件:
①fX|Y(x|y)≥0,-∞<x<+∞;
②![]()
定义3.3.3是很合理的,若(X,Y)为二维连续型随机变量,概率密度为f(x,y)。对某个固定的y,当f(x,y)在(x,y)处关于y 连续、fY(y)在y 处连续且fY(y)>0时,有
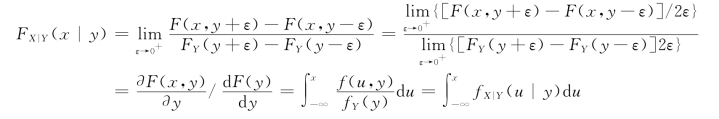
从定义3.3.3还可得到f(x,y)=fX(x)fY|X(y|x)=fY(y)fX|Y(x|y)。因此,由边缘分布或条件分布单独都不能确定联合分布,但在二者都已知的条件下完全可以确定联合分布。此公式也称作密度乘法公式。
例3.3.1 设二维随机变量的概率密度为
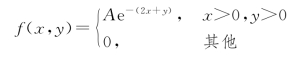
试求:
(1)常数A 的值;
(2)分布函数F(x,y);
(3)P{Y≤X}。
解 (1)由![]() 得
得
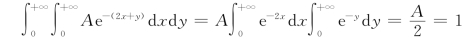
所以A=2。
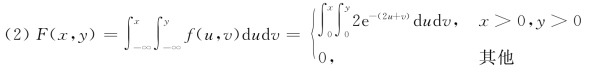
因此
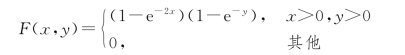
(3)设G:y≤x,即直线y=x 的下方部分(图3.3.1),则
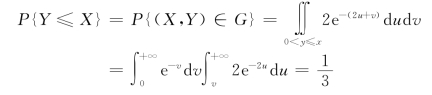
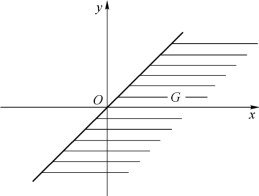
图3.3.1
例3.3.2 假设G={(x,y):x2+y2≤r2}是以原点为圆心、半径为r的圆(图3.3.2);已知X 和Y 的联合概率密度为f(x,y),在圆G 上为常数,在圆G 外f(x,y)=0。试求:
(1)联合概率密度f(x,y);
(2)(X,Y)的边缘概率密度,即X 和Y 的概率密度fX(x)和fY(y);
(3)Y 关于X=x 的条件概率密度fY|X(y|x)。
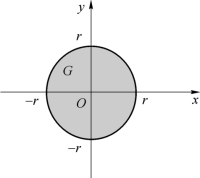
图3.3.2
解 (1)由于圆G 的面积等于πr2,可见
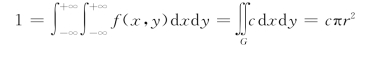
从而![]() 于是,得X 和Y 的联合概率密度为
于是,得X 和Y 的联合概率密度为
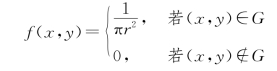
(2)当|x|>r时,显然fX(x)=0。设|x|≤r,则X 的密度为
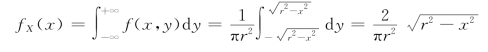
于是,得X 的概率密度为
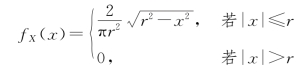
同理可得Y 的概率密度为
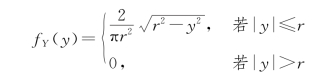
(3)对任意|x|<r,fX(x)>0,则Y 关于X=x 的条件概率密度为(https://www.xing528.com)
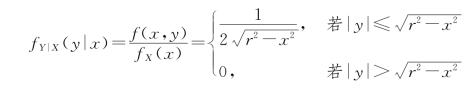
这时,称(X,Y)在区域G 上服从二维均匀分布。
一般地,设G 是平面上的有界区域,其面积为A≠0。若二维随机变量(X,Y)具有概率密度
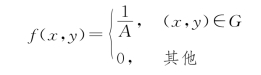
则称(X,Y)在G 上服从均匀分布,记作(X,Y)~U(G)。
注意:若(X,Y)~U(G),X 和Y 的分布一般不是均匀分布,但当G 为矩形区域时,即G 为区域![]() }时,则X~U[a,b],Y~U[c,d]。可无论G 为平面上的任何有界区域,它们之中一个关于另一个的条件分布都是均匀分布。
}时,则X~U[a,b],Y~U[c,d]。可无论G 为平面上的任何有界区域,它们之中一个关于另一个的条件分布都是均匀分布。
例3.3.3 设数X 在区间(0,1)上随机地取值。当观察到X=x(0<x<1)时,数Y 在区间(x,1)上随机地取值。求Y 的概率密度fY(y)。
解 由题意知X 服从(0,1)上的均匀分布,即
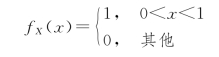
对任意给定的值x(0<x<1),在X=x 条件下Y 服从(x,1)上的均匀分布,即
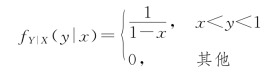
从而,X 和Y 的联合概率密度为
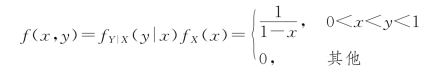
于是
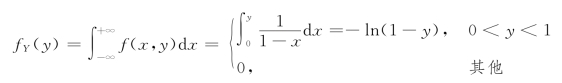
例3.3.4 假设随机变量X 和Y 的联合概率密度为

(1)求X 和Y 的联合分布函数F(x,y);
(2)求X 和Y 的分布函数FX(x)和FY(y)。
解 (1)当x<0或y<0时显然F(x,y)=0;当x≥1或y≥1时显然F(x,y)=1。对于0≤x≤1,0≤y≤1,
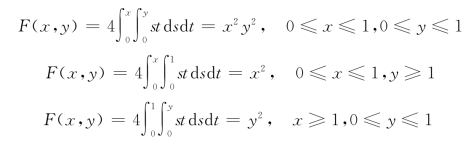
于是

(2)X 和Y 的分布函数FX(x)和FY(y)是F(x,y)的边缘分布函数。易见,当x<0时,FX(x)=0;当x>1时,FX(x)=1;现在设0≤x≤1,有
![]()
于是,X 的分布函数
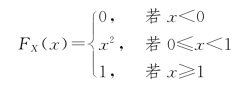
类似可得Y 的分布函数
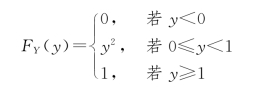
例3.3.5 设二维随机变量(X,Y)的概率密度为
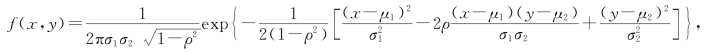
![]()
其中μ1,μ2,σ1,σ2,ρ都是常数,且σ1>0,σ2>0,-1<ρ<1,则称(X,Y)服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布,记作(X,Y)~N(μ1,μ2,σ21,σ22,ρ)。试求二维正态随机变量的(1)边缘概率密度;(2)条件概率密度。
解 (1)由于![]() 用公式
用公式![]() 则有
则有
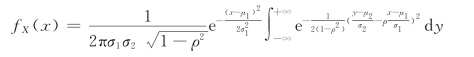
令![]() 于是
于是

同理,
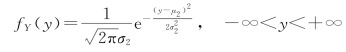
(2)对固定的x,X=x 时,Y 的条件概率密度为
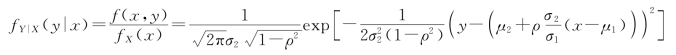
因此,二维正态分布的条件分布为一维正态分布![]()
同理,对固定的y,Y=y 时,X 的条件概率密度为
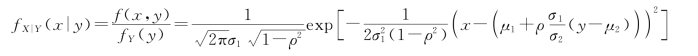
即条件分布为一维正态分布![]()
注意
①二维正态分布的两个边缘分布及条件分布都是一维正态分布,并且两个边缘分布都不依赖于参数ρ,这也说明,一般来说边缘分布不能确定联合分布。看下面的例子:
设随机变量(X,Y)的概率密度
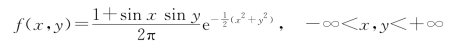
由边缘密度的公式,有
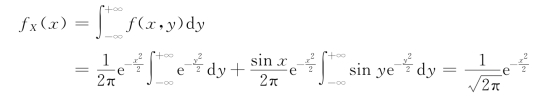
同理,fY(x)=![]() 可见X 和Y 都服从标准正态分布,但是X 和Y 的联合分布却不是二维正态分布。
可见X 和Y 都服从标准正态分布,但是X 和Y 的联合分布却不是二维正态分布。
②可以证明,若二维随机变量(X,Y)服从二维正态分布,则X 和Y 的线性组合仍然服从正态分布,即对于任何实数a和b(至少一个不为0),有
![]()
特别地,![]() 但若X 和Y 均服从正态分布,它们的线性组合未必服从正态分布。
但若X 和Y 均服从正态分布,它们的线性组合未必服从正态分布。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




