二维离散型随机变量的概率论与数理统计

同一维随机变量一样,我们主要研究离散型和连续型两大类二维随机变量。对这两类随机变量,同样可以用类似一维随机变量的分布律及概率密度来研究。

定义3.2.1 如果二维随机变量(X,Y)的所有可能值是有限个或无限可列个,则称(X,Y)为二维离散型随机变量。

定义3.2.2 设二维离散型随机变量(X,Y)的全部可能值为(xi,yj),i=1,2,…,j=1,2,…。(X,Y)取各个可能值的概率为

称上式为二维离散型随机变量(X,Y)的分布律或概率分布,也称为X 与Y 的联合分布律或联合概率分布。

容易看出,二维随机变量的分布律中pij满足下面两个基本条件:

①pij≥0,i=1,2,…,j=1,2,…;

②

其实,若有一个数列{pij}满足如上两条,它一定可作为某一二维离散型随机变量的分布律。

为方便直观,也可用表3.2.1来表示二维离散型随机变量(X,Y)的分布。

表3.2.1

有时,也可表示为

特别是当(X,Y)的取值较少时,用表3.2.1表示更方便。

与一维情形一样,也可得到二维离散型随机变量的分布函数和分布律有如下关系。

其中(xi,yj)为(X,Y)的可能取值点。

例3.2.1 设随机变量X 和Y 的联合概率分布如表3.2.2所示。

表3.2.2

试求X 和Y 的联合分布函数F(x,y)。

解 可求得

例3.2.2 设随机变量X 和Y 的联合概率分布如表3.2.3所示。

表3.2.3

试求a的值。

解 由,所以a=

下面讨论二维离散型随机变量的边缘分布及条件分布。

定义3.2.3 设(X,Y)为二维离散型随机变量,称分量X(或Y)的分布律为(X,Y)关于X(或Y)的边缘分布律。

设(X,Y)的联合分布律为

那么,关于X 的边缘分布律为

同理,关于Y 的边缘分布律为

联合分布律与边缘分布律放在一起如表3.2.4所示。

表3.2.4

因为随机变量X,Y 的取值及其取值的概率正好居于表3.2.4的四周,这也是边缘分布名称的由来。

定义3.2.4 设(X,Y)是二维离散型随机变量,对于固定的j,P{Y =yj}＞0,则称

为在Y =yj条件下X 的条件分布律,上述概率也记为

同样定义X =xi 条件下Y 的条件分布律。

由此定义可知,和分布律一样,条件分布律也满足如下两个基本条件:(https://www.xing528.com)

①P{X =xi|Y =yj}≥0, i=1,2,…;

②

有兴趣的读者可按定义证明,当P{Y =yj}＞0,P{X =xi}＞0时,二维离散型随机变量(X,Y)的条件分布函数与条件分布律的关系为

例3.2.3 袋中装有2只白球及3只黑球,从袋中先后任取两球。定义随机变量

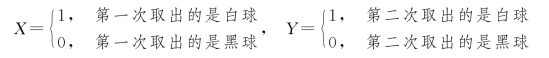
求(X,Y)的联合分布律及各边缘分布律。

解 对有放回方式取球和不放回方式取球这两种情形分别考虑。

(1)以有放回方式取球时,(X,Y)的全部可能值为(i,j),其中i=0或1,j=0或1。由乘法公式,有

同理可得

关于X 的边缘分布律为

关于Y 的边缘分布律为

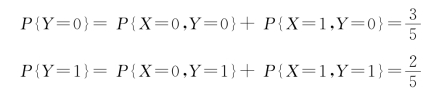
上面得到的(X,Y)的分布律及各边缘分布律如表3.2.5所示。

表3.2.5

(2)以不放回方式取球时,同上方法可得(X,Y)的分布律及各边缘分布律如表3.2.6所示。

表3.2.6

此例中在两种不同取球方式下得到的两个二维随机变量的分布律不同,但是,它们的边缘分布律却是一样的。因此,一般来说,边缘分布不能决定联合分布。

例3.2.4 已知随机变量X 和Y 的概率分布为

而且P{XY=0}=1。求X 和Y 的联合分布律。

解 由条件P{XY=0}=1,可见P{XY≠0}=0,故P{X=1,Y=-1}=P{X=1,Y=1}=0。在表3.2.7中,首先将X 的分布和Y 的分布——两个边缘分布填入表的边缘;再将(-1,1)和(1,1)的概率0填入表中,则容易求出X 和Y 的联合分布律。

表3.2.7

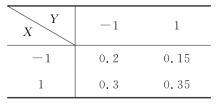
例3.2.5 假设随机变量X 和Y 的联合概率分布为

(1)分别求X 和Y 的概率分布;

(2)求Y 关于X 的条件概率分布。

解 易见X 有0,1,2共3个可能值,而Y 有1,2共2个可能值。

(1)X 的概率分布为

Y 的概率分布为

(2)Y 关于X=0的条件概率分布为

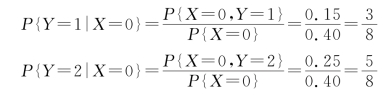
Y 关于X=1的条件概率分布为

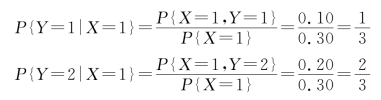
Y 关于X=2的条件概率分布为