随机变量函数的分布-概率论与数理统计

设y=g(x)是连续函数或分段连续函数,Y=g(X)作为随机变量X 的函数也是随机变量。如何根据随机变量X 的概率分布求其函数Y=g(X)的概率分布? 一般方法是:设法将Y=g(X)的分布函数通过X 的概率分布表示:

基于这种表示,在许多情形下可以求出Y=g(X)的概率分布。

(1)离散型情形

设X 是离散型随机变量,其一切(有限或可数个)可能值为{x1,x2,…}。为求随机变量Y=g(X)的概率分布,首先由函数关系y=g(x)列出Y 的一切可能值{y1,y2,…},然后分别求概率P{Y=yj}(j=1,2,…)。这时,

①已知P{X=xi}=pi(i=1,2,…),若函数y=g(x)的一切可能值两两不等,则

就是Y 的概率分布;

②若对于某些X 的可能值{xk1,…,xkr},y=g(xkj)等于同一值yk,则

(2)连续型情形

设X 是连续型随机变量,则随机变量Y=g(X)可能是连续型的,也可能是离散型的。

①若函数y=g(x)只有有限或可数个可能值,按上述离散型情形处理;

如X 的概率密度为f(x),g(x)=,则Y=g(X)服从0-1分布。

②若函数y=g(x)所有可能值的集合是(有限或无限)区间,则一般先求Y 的分布函数F(x)再求导数F′(x),即可得到Y=g(X)的概率密度f(x)。

例2.4.1 设随机变量X～B(3,0.7),求:

(1)随机变量Y1=X2 的概率分布;

(2)随机变量Y2=X2-2X 的概率分布;

(3)随机变量Y3=3X-X2 的概率分布。

解 由X～B(3,0.7)知X 的概率分布为

根据X 的概率分布列出表2.4.1。

表2.4.1

由表2.4.1得Y1=X2 的概率分布为

随机变量Y2=X2-2X 的概率分布为

(www.xing528.com)

随机变量Y3=3X-X2 的概率分布为

例2.4.2 已知随机变量X 服从标准正态分布,求Y=X2 的概率密度。

解 以F(y)和f(y)分别表示Y 的分布函数和概率密度。当y≤0时显然F(y)=0;对于y＞0,有

对y 求导,得

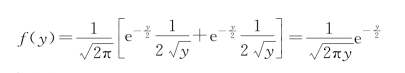
于是,Y=X2 的概率密度为

特别地,假设y=g(x)处处可导且是严格单调的连续函数,(c,d)是函数y=g(x)的值域,x=h(y)是y=g(x)的反函数;X 是连续型随机变量,其概率密度为f(x),则Y 也是连续型随机变量,其概率密度p(y)通过f(x)表示为

证明 以G(y)表示随机变量Y=g(X)的分布函数。若y=g(x)为增函数,则h(y)也是增函数,故h′(y)＞0;若y=g(x)为减函数,则h(y)也是减函数,故h′(y)＜0。显然,当y≤c时,G(y)=0;当y≥d 时,G(y)=1。先设y=g(x)为增函数,对于c＜y＜d,有

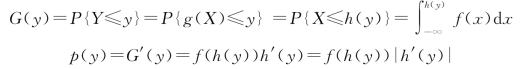
当y=g(x)为减函数时,对于c＜y＜d,有

综上所述,结论得证。

例2.4.3 设X 的密度函数为试求Y=eX 的概率密度fY(y)。

解 方法1——公式法:y=ex 单调增加,且反函数为x=lny,y＞0,于是

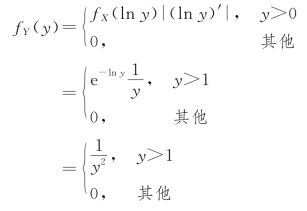
方法2——分布函数法:

①当y≤0时,FY(y)=0。

②当0＜y≤1时

③当y＞1时

故

从而